Question

How do you graph $y = \dfrac{1}{5}x - 3$ by plotting points?

Answer 1

To graph an equation by plotting points, the easiest way to find points on the line of the given equation $y = \dfrac{1}{5}x - 3$ is to convert the given equation in point slope form to slope intercept form: $y = mx + b$, where m is the slope, and b is the y-intercept. In order to do this, solve the point slope equation for y, then consider any x values to graph the solution.

Complete step by step solution:
Let us write the given linear equation:
$y = \dfrac{1}{5}x - 3$
To graph the equation by plotting points, we need to create a table of values that satisfies the given equation:
$f\left( x \right) = x$,
$f\left( x \right) = \left( {\dfrac{1}{5}} \right) \cdot x$,
$f\left( x \right) = \left[ {\left( {\dfrac{1}{5}} \right) \cdot x} \right] - 3$
for easy comprehension.
Examine the graph for $y = f\left( x \right) = x$.

x	$f\left( x \right) = x$
-2	-2
-1	-1
0	0
1	1
2	2

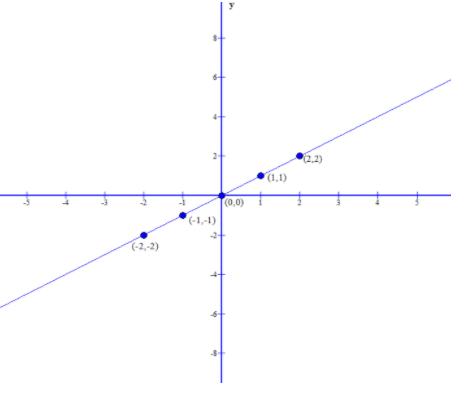
The graph obtained is Slope-Intercept form: $y = mx + b$,
where m is the slope, and b is the y-intercept.
This is of the form $y = 1 \cdot x + 0$, where Slope(m)=1 and y-intercept=0
Remember that the Slope(m) is the constant ratio that compares the change in y values over the change in x values between any two points. y-intercept is the coordinate point where the graph crosses the y-axis.
Now let us Examine the graph for $f\left( x \right) = \left( {\dfrac{1}{5}} \right) \cdot x$

x	$\dfrac{1}{5}x$
-2	-0.4
-1	-0.2
0	0
1	0.2
2	0.4

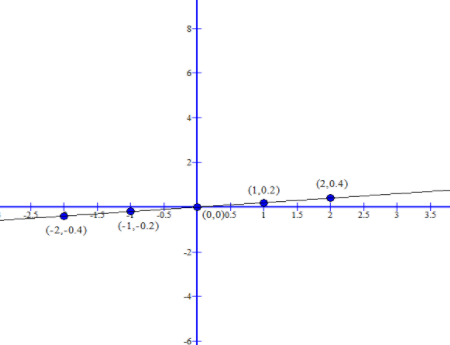
The graph obtained is Slope-Intercept form: $y = mx + b$,
In which,
Slope(m) = $\dfrac{1}{5}$, and y-intercept is 0.
We need to create data table for x and corresponding y values:
$y = f\left( x \right) = \dfrac{1}{5}x - 3$

x	y
-5	-4.00
-4	-3.80
-3	-3.60
-2	-3.40
-1	-3.20
0	-3.00
1	-2.80
2	-2.60
3	-2.40
4	-2.20
5	-2.00

Now construct the graph using these data values.

Examine the graph of $y = f\left( x \right) = \dfrac{1}{5}x - 3$ as:

x	$\dfrac{1}{5}x - 3$
-2	-3.4
-1	-3.2
0	-3
1	-2.8
2	-2.6

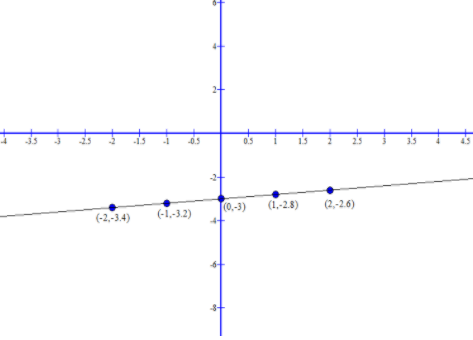
The equation is Slope-Intercept form: $y = mx + b$, and the slope obtained is:
Slope(m) = $\dfrac{1}{5}$, and y-intercept is $\left( {0, - 3} \right)$.

Note:
In slope intercept form; very often, linear-equation word problems deal with changes over the course of time i.e., $y = mx + b$ the number b is the coordinate on the y-axis where the graph crosses the y-axis and also, we can solve the given equation using intercept form i.e., when x = 0, the corresponding y-value is the y-intercept. In the particular context of word problems, the y-intercept (that is, the point when x = 0) also refers to the starting value.