Question

How do you graph $y = \dfrac{1}{4} + \sin x$ ?

Answer 1

This question deals with the properties of $\sin$ . Here we will use different characteristics of the trigonometric function.
$\sin$ function is a periodic function with a period of $2\pi$ .the domain of $\sin$ function is defined in the interval of $\left( { - \infty ,\infty } \right)$ and the range of $\sin$ function is $\left[ { - 1,1} \right]$ . $\sin$ is an odd function which means its graph will be symmetric about origin.an odd function is defined as a function which is symmetric about the origin. The mathematical expression for odd function is defined as $f\left( { - x} \right) + f\left( x \right) = 0$ ,the $x -$ intercept of $\sin$ function is $k\pi$ ,where $k$ is an integer and the $y -$ intercept of the function is 0.the maximum points of the function are $\left( {\dfrac{\pi }{2} + 2k\pi ,1} \right)$ where $k$ is an integer and the minimum points of the function are $\left( {\dfrac{{3\pi }}{2} + 2k\pi , - 1} \right)$ where $k$ is an integer.
The function over one period and from 0 to $2\pi$ is increasing in the interval $\left( {0,\dfrac{\pi }{2}} \right)$ and $\left( {\dfrac{{3\pi }}{2},2\pi } \right)$ ,and decreasing in the interval $\left( {\dfrac{\pi }{2},\dfrac{{3\pi }}{2}} \right)$ .

Complete step by step answer:
Step: 1 the normal $\sin x$ graph makes a wave around the $x -$ axis repeating itself every $2\pi$ .
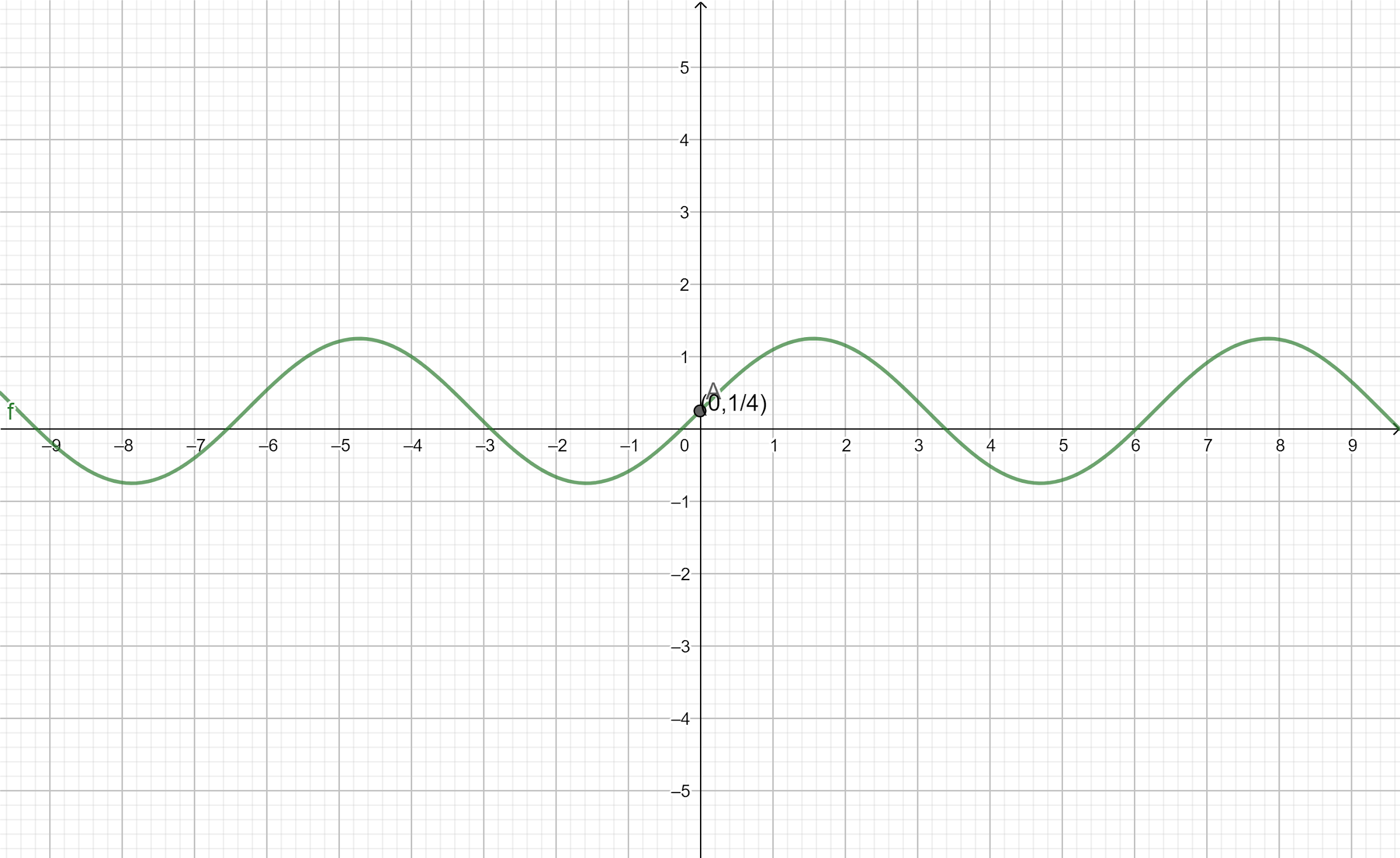
To draw the graph of the function, make $x -$ axis and $y -$ axis with origin (0,0).
Plot the graph of $\sin x$ function on the graph with $x -$ axis.
Shift the graph of $\sin x$ function by $\dfrac{1}{4}$ towards up on the $y -$ axis.
Adding $\dfrac{1}{4}$ to every point we will find the graph of the function oscillating around the line passing through $y = \dfrac{1}{4}$ .

Note:
Always try to remember the basic properties of $\sin$ function. Find the period, rang, and domain of the $\sin$ function. Start plotting the graph from origin. Check either the function is increasing or decreasing .Student must know the property of symmetric function, shift the graph of $\sin x$ up by $\dfrac{1}{4}$ unit passing through the line $y = \dfrac{1}{4}$ .