Question

How do you graph $y = \dfrac{1}{3}x + 2$ by plotting points?

Answer 1

Here, in this question we are asked to graph the line $y = \dfrac{1}{3}x + 2$. Before starting solving the question, we will have to compare it with slope-intercept form i.e., $y = mx + c$. Here, $c = 2$ which means that the intercept on the $y$-axis is $2$ and $m = \dfrac{1}{3}$ which means that the slope of the line is $\dfrac{1}{3}$.

Complete step by step solution:
The given equation of the line is$y = \dfrac{1}{3}x + 2$. We are supposed to put the equation in slope intercept form i.e.,$y = mx + c$. Here, we get $y = \dfrac{1}{3}x + 2$, so we get $m = \dfrac{1}{3}$ and $c = 2$. Now, we will have to make a table of values, which can be done by using different values of $x$.

Here, when we put $x = 3$, we get $y = 3$. So, we get point $\left( {3,3} \right)$. When we put $x = 6$, we get $y = 4$. So, we get point$\left( {6,4} \right)$.

$x$	$3$	$6$
$y$	$3$	$4$
Point $\left( {x,y} \right)$	$\left( {3,3} \right)$	$\left( {6,4} \right)$

So, now we have points: $\left( {3,3} \right)$,$\left( {6,4} \right)$.
Now, we draw our axes for $x$ and $y$. We have to choose the appropriate scale and mark the values on the $x$ and $y$ axis. Mark all the three points and draw a straight line through these points.

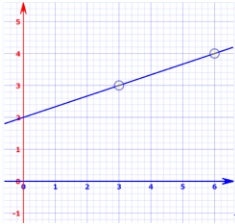
Therefore, we have our required graph.
Note: In order to solve such questions, we first need to analyse what is given to us. The given equation $y = \dfrac{1}{3}x + 2$ is a simple linear equation. To graph a linear equation, we have to draw a line in a $2 - D$ plane. Students should keep in mind that every linear equation represents a straight line. In order to check if the points calculated are correct or not, just put their values in the given equation if L.H.S=R.H.S then, the points are correct.