Question

How do you graph $y = \dfrac{1}{2}x + 4$?

Answer 1

Here we will plot the graph of the given equation by using the Intercept form. First, we will compare the given equation with the standard intercept form to get the value of the slope and $y$-intercept. We will substitute different values of $x$ or $y$ in the equation to get corresponding values of $y$ or $x$. From this we will get coordinate points and using these points we will draw the required graph.

Complete step by step solution:
The equation of line is given as,
$y = \dfrac{1}{2}x + 4$……$\left( 1 \right)$
Comparing the equation with the intercept form $y = mx + b$, we get
$\begin{array}{l}m = \dfrac{1}{2}\\\b = 4\end{array}$
Now we will substitute different values of $x$ in the given equation to find various coordinate points.
Substituting $x = 0$ in equation, we get
$y = \dfrac{1}{2} \times 0 + 4$
Multiplying the terms, we get
$\Rightarrow y = 4$
So, one of the coordinate points is $\left( {0,4} \right)$.
Next, let $y = 0$ be another point substituting it in equation $\left( 1 \right)$, we get
$\begin{array}{l}0 = \dfrac{1}{2}x + 4\\\ \Rightarrow \dfrac{1}{2}x = - 4\end{array}$
Multiplying both sides by 2, we get
$\Rightarrow x = - 8$
So our second coordinate is $\left( { - 8,0} \right)$
Now, we will plot the two points in the graph and join them straight.

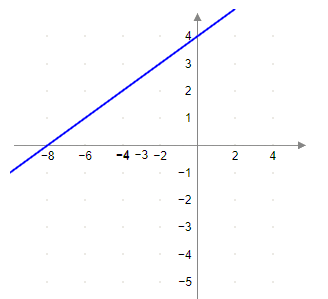
The graph of equation $y = \dfrac{1}{2}x + 4$ is plotted as above.

Note:
A-Line is a one-dimensional figure that extends endlessly in both directions. It is also described as the shortest distance between any two points. There are many ways to draw the graph of the equation such as Point-slope Form, Intercept Form, Determinant Form, and many others. The Form we are using depends on the data we have. The scale can change as per the requirement so that the graph is plotted easily.