Question

How do you graph $y = - \dfrac{1}{2}$ using intercepts?

Answer 1

Linear equations in the form $y = a$ have no $x$-intercept. The linear equation $y = a$ is a line parallel to $x$-axis that intercept $y$-axis at point $\left( {0,a} \right)$. Therefore, the graph is a line parallel to the x-axis that cuts the y-axis at negative of half for the given equation.

Complete step-by-step solution:
The given equation $y = - \dfrac{1}{2}$ can be written as shown below.
$\Rightarrow y = - \dfrac{1}{2} + 0x$ …… (1)
We are asked to draw the graph using the intercepts.
It is observed that a given equation is one of the equations of a straight line. We know this fact because both x and y terms in the equation are of power 1 (so they are not squared or square rooted terms).
We can simplify the given equation, so that our calculation becomes easier.
We find the points of intercepts and then draw a line through them as at least two points are needed to draw a unique line.
Finding the $x$-intercept:
The line crosses the x-axis at $y = 0$.
Taking $y = 0$ in the equation (1) we get,
$\Rightarrow 0 = - \dfrac{1}{2} + 0x$
This can be written as,
$\Rightarrow 0 = - \dfrac{1}{2}$
This is a false equation. It implies that our substitution $y = 0$ is not true.
This further implies that the line of a given equation does not have a $x$-intercept, in other word line is parallel to $x$-axis.
Finding the $y$-intercept:
The line crosses the y-axis at $x = 0$.
Taking $x = 0$ in the equation (1) we get,
$\Rightarrow y = - \dfrac{1}{2} + 0\left( 0 \right)$
This can be written as,
$\Rightarrow y = - \dfrac{1}{2}$
So the point is $\left( {0, - \dfrac{1}{2}} \right)$.
Hence the line does not have $x$-intercept and the $y$-intercept is $\left( {0, - \dfrac{1}{2}} \right)$.
Now, we plot the graph on the x-y plane such that it cuts the y –axis at $- \dfrac{1}{2}$ and parallel to x-axis as shown in the below figure.

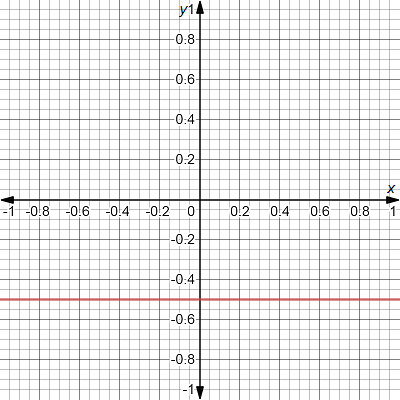
Note that the graph is a straight line parallel to x-axis.

Note: Students must remember that to obtain the $x$-intercept, we set the value of y equal to zero and find the point. Then, to obtain the $y$-intercept, we set the value of x equal to zero and find the point. Then from obtained $(x,y)$ points we plot a graph of the given equation in the x-y plane.