Question

How do you graph $y = - \csc x$

Answer 1

Graphing the negative of a function essentially implies flipping the function about the X-axis. This question can be approached similarly. We can start by drawing the graph of $y = \csc x$ and then try flipping it around the X-axis.

Complete Step by Step Solution:
We should start solving the question by drawing the graph of $y = \csc x$.
The graph of $y = \csc x$ is as follows:

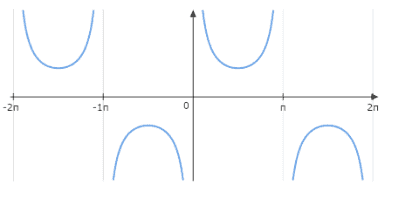
The range of the x-axis is set from $- 2\pi$ to $2\pi$. An asymptote of a curve can be described as a line such that the distance between the curve and line approaches zero when either one or both of the x and y coordinates tend to infinity.
The graph of $y = \csc x$ has asymptotes at the point $n\pi$ . n is an integer.
When $x = \dfrac{\pi }{2} \pm 2n\pi$ , then the value of $y = 1$
When $x = \dfrac{{3\pi }}{2} \pm 2n\pi$ , then the value of $y = - 1$
The negative sign is used in order to change the sign of the y values. Thus, the positive values of y become negative and the negative values of y become positive. In this case, we’re essentially flipping the equation around the X-axis.
Thus, the graph of $y = - \csc x$ can be drawn as follows:

Note:

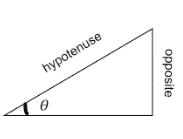
The cosecant of any angle, $\theta$ in a right-angled triangle is defined as:
$\csc \theta = \dfrac{{length\left( {hypotenuse} \right)}}{{length(opposite)}}$
Cosecant of an angle can be related to the sine of the angle in the following manner:
$\csc \theta = \dfrac{1}{{\sin \theta }}$