Question

How do you graph $y = \cot x$?

Answer 1

We need to graph the given function. We will use the domain and some values of $x$ lying between $- 2\pi$ and $2\pi$ to find some values of $y$. Then, we will observe the behavior of the value of $y$, and use it and the coordinates obtained to graph the function.

Complete step-by-step solution:
The domain of the function $y = \cot x$ is given by \left\\{ {x:x \in R{\rm{ and }}x \ne n\pi ,n \in Z} \right\\}. This means that the cotangent of any multiple of $\pi$ does not exist.
The graph of the cotangent function reaches arbitrarily large positive or negative values at these multiples of $\pi$.
Now, we will find some values of $y$ for some values of $x$ lying between $- 2\pi$ and $2\pi$.
Substituting $x = - \dfrac{{3\pi }}{2}$ in the function $y = \cot x$, we get
$\begin{array}{l}y = \cot \left( { - \dfrac{{3\pi }}{2}} \right)\\\ \Rightarrow y = 0\end{array}$
Substituting $x = - \dfrac{\pi }{2}$ in the function $y = \cot x$, we get
$\begin{array}{l}y = \cot \left( { - \dfrac{\pi }{2}} \right)\\\ \Rightarrow y = 0\end{array}$
Substituting $x = \dfrac{\pi }{2}$ in the function $y = \cot x$, we get
$\begin{array}{l}y = \cot \left( {\dfrac{\pi }{2}} \right)\\\ \Rightarrow y = 0\end{array}$
Substituting $x = \dfrac{{3\pi }}{2}$ in the function $y = \cot x$, we get
$\begin{array}{l}y = \cot \left( {\dfrac{{3\pi }}{2}} \right)\\\ \Rightarrow y = 0\end{array}$
The value of $y$ at $x = 2\pi ,\pi ,0,\pi ,2\pi$ is infinite.
Arranging the values of $x$ and $y$ in a table and writing the coordinates, we get

$x$	$y$
$- 2\pi$	$\infty$
$- \dfrac{{3\pi }}{2}$	$0$
$- \pi$	$\infty$
$- \dfrac{\pi }{2}$	$0$
$0$	$\infty$
$\dfrac{\pi }{2}$	$0$
$\pi$	$\infty$
$\dfrac{{3\pi }}{2}$	$0$
$2\pi$	$\infty$

The value of $y = \cot x$ decreases from $\infty$ to 0 at $x = - \dfrac{{3\pi }}{2}$, and then to $- \infty$ in the interval $\left( { - 2\pi , - \pi } \right)$.
Similarly, the value of $y = \cot x$ decreases from $\infty$ to 0 at $x = - \dfrac{\pi }{2},\dfrac{\pi }{2},\dfrac{{3\pi }}{2}$, and then to $- \infty$ in the intervals $\left( { - \pi ,0} \right)$, $\left( {0,\pi } \right)$, and $\left( {\pi ,2\pi } \right)$.
Now, we will use the points $\left( { - \dfrac{{3\pi }}{2},0} \right)$, $\left( { - \dfrac{\pi }{2},0} \right)$, $\left( {\dfrac{\pi }{2},0} \right)$, $\left( {\dfrac{{3\pi }}{2},0} \right)$ and the behaviour of the value of $y = \cot x$ to graph the function.
Therefore, we get the graph

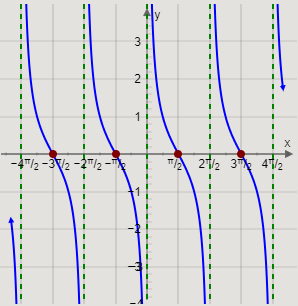
This is the required graph of the function $y = \cot x$.

Note:
The period of the function $y = \cot x$ is $\pi$. This means that the graph of $y = \cot x$ will repeat for every $\pi$ distance on the $x$-axis. It can be observed that the pattern and shape of the graph of $y = \cot x$ is the same from $- 2\pi$ to $- \pi$, from $- \pi$ to 0, from 0 to $\pi$, and from $\pi$ to $2\pi$. The range of cotangent functions is from $- \infty$ to $\infty$. As tangent function is a reciprocal function cotangent function, so their graph faces opposite to each other.