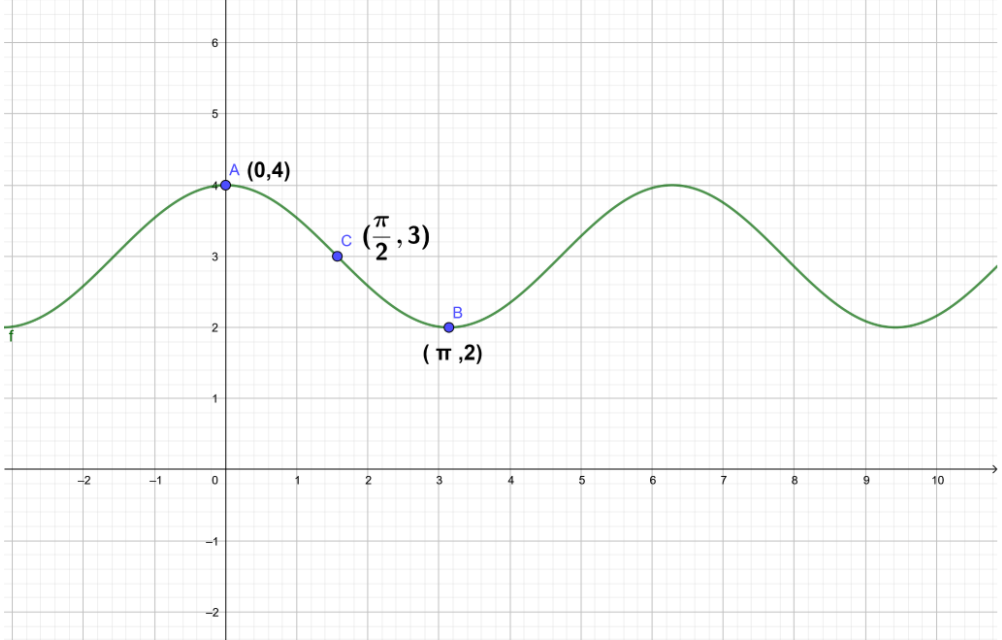
Question

How do you graph $y = \cos x + 3$?

Answer 1

We need to graph the function $y = \cos x + 3$. On observing this function, we see that this function is of the form $y = f\left( x \right) + a$, where $a$ is a constant. To sketch the graph of such functions, we first sketch the graph of $y = f\left( x \right)$. Now, since $a$ is added to the term, the graph of $y = f\left( x \right)$ when shifted $a$ units upward, gives the graph of $y = f\left( x \right) + a$. Let us now use this procedure to sketch the graph of the given function.

Complete step by step answer:
We need to sketch the graph of the function $y = \cos x + 3$.
Comparing $y = \cos x + 3$ with $y = f\left( x \right) + a$, we get
$\Rightarrow f\left( x \right) = \cos x$
$\Rightarrow a = 3$
Now, to sketch the graph of $y = \cos x + 3$, we first sketch the graph of $y = \cos x$.
Let us sketch the graph of $y = \cos x$.

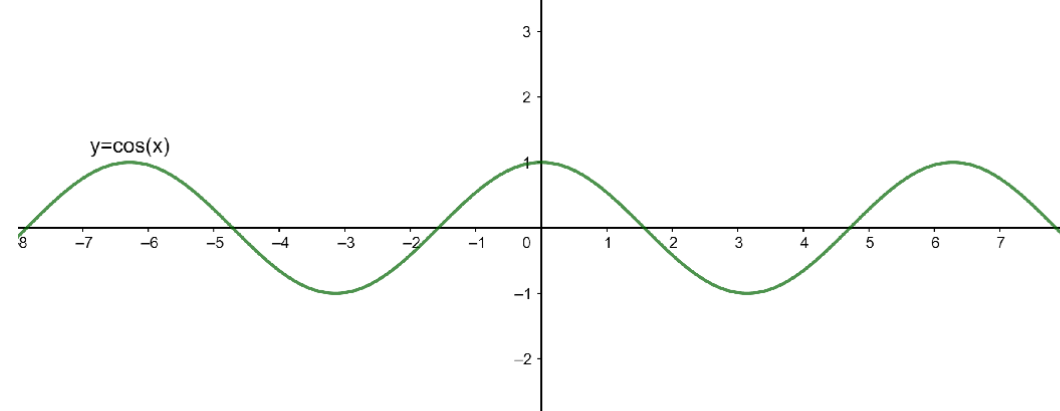
The above graph is for the function $y = \cos x$ but we need to sketch the graph of $y = \cos x + 3$.Now, since $a = 3$, we need to shift the graph of $y = \cos x$ three units upwards.Shifting the graph three units upward, we get the following graph

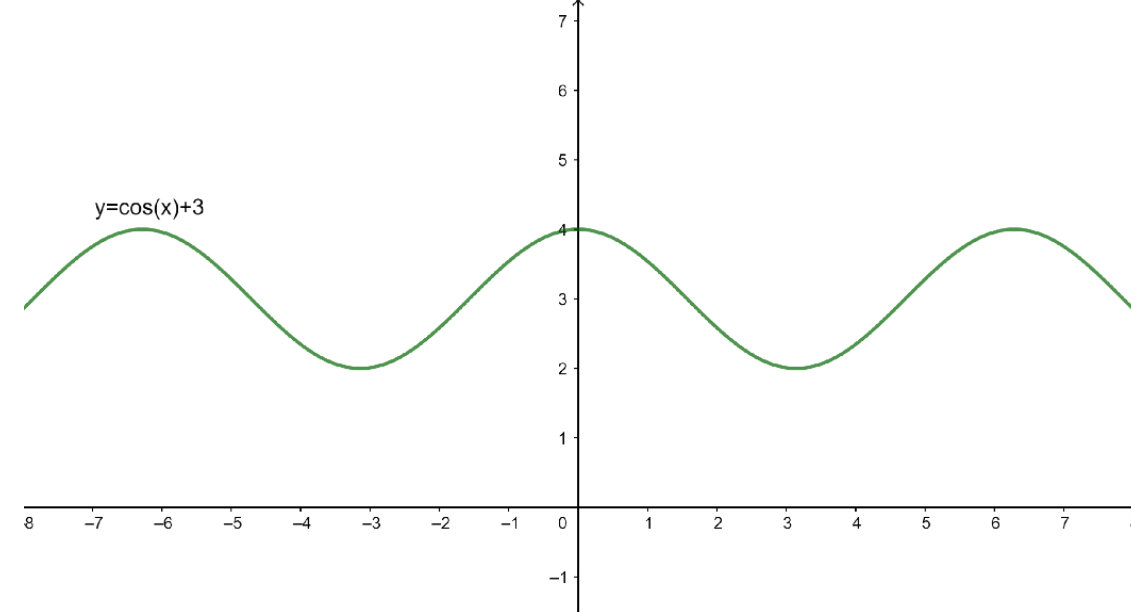
The graph obtained by shifting the graph of $y = \cos x$ three units upward is the graph of the function $y = \cos x + 3$. Hence, the graph above is the required graph.

Note: We can also sketch the graph directly by putting the values of $x$ and obtaining the corresponding values of $y$, then joining the points on the cartesian plane and obtaining the required graph. If we were given the function of the form $y = f\left( x \right) - a$, where $a$ is a constant, then we need to shift the graph of $y = f\left( x \right)$ downward by $a$ units.
For example: Let us assume the value of x as zero. Then, we have,
$y = \cos \left( 0 \right) + 3$
We know that the value of $\cos \left( 0 \right)$ is $1$. So, we get,
$\Rightarrow y = 1 + 3$
$\Rightarrow y = 4$

Similarly, if value of x is $\pi$, we get,
$y = \cos \left( \pi \right) + 3$
We know that the value of $\cos \left( \pi \right)$ is $\left( { - 1} \right)$. So, we get,
$\Rightarrow y = - 1 + 3$
$\Rightarrow y = 2$
For x equals $\left( {\dfrac{\pi }{2}} \right)$, we have,
$y = \cos \left( {\dfrac{\pi }{2}} \right) + 3$
We know that the value of $\cos \left( {\dfrac{\pi }{2}} \right)$ is zero. So, we get,
$\Rightarrow y = 0 + 3$
$\Rightarrow y = 3$
Hence,we plot these points on the graph and join to get the graphical representation of the given function.