Question

How do you graph $y = \cos \left( {2x} \right)$ over the interval $0 \leqslant x \leqslant 360$?

Answer 1

In this problem we have given a trigonometric function over some interval and we asked to draw a graph using the given trigonometric function over some interval and also we have given some period. Then, using the given trigonometric function we can write some points to plot and if we join those points with a smooth cure.

Complete step-by-step solution:
Given trigonometric function is $y = \cos \left( {2x} \right)$
The value of $\cos x$ corresponds to the $x$-values, so those key points are angles, $x$-values or the points of the $\cos$ function $\left( {0,1} \right),\left( {\dfrac{\pi }{2},0} \right),\left( {\pi , - 1} \right),\left( {\dfrac{{3\pi }}{2},0} \right),\left( {2\pi ,1} \right)$
The points of the $\cos$ function can also be written as $\left( {0,1} \right),\left( {90,0} \right),\left( {180, - 1} \right),\left( {270,0} \right),\left( {360,1} \right)$
The period of a period function is the interval of $x$-values on which the cycle of the graph that is repeated in both directions lies.
Here the period is $2x$.
But because it $2x$ the period is shortened. It will reach the point $0$ after only $45$, the $- 1$ after $90$, etc.
So the points are now:
$\left( {0,1} \right),\left( {45,0} \right),\left( {90, - 1} \right),\left( {135,0} \right),\left( {180,1} \right),\left( {225,0} \right),\left( {270, - 1} \right),\left( {315,0} \right),\left( {360,1} \right)$
These points can also be written as $\left( {0,1} \right),\left( {\dfrac{\pi }{4},0} \right),\left( {\dfrac{\pi }{2}, - 1} \right),\left( {\dfrac{{3\pi }}{4},0} \right),\left( {\pi ,1} \right),\left( {\dfrac{{5\pi }}{4},0} \right),\left( {\dfrac{{3\pi }}{2}, - 1} \right),\left( {\dfrac{{7\pi }}{4},0} \right)$and$\left( {2\pi ,1} \right)$. Then we join these points in the graph.
The vertical axis of the graph lies between $1$ to $- 1$.
The graph of the trigonometric function $y = \cos \left( {2x} \right)$ is given below.

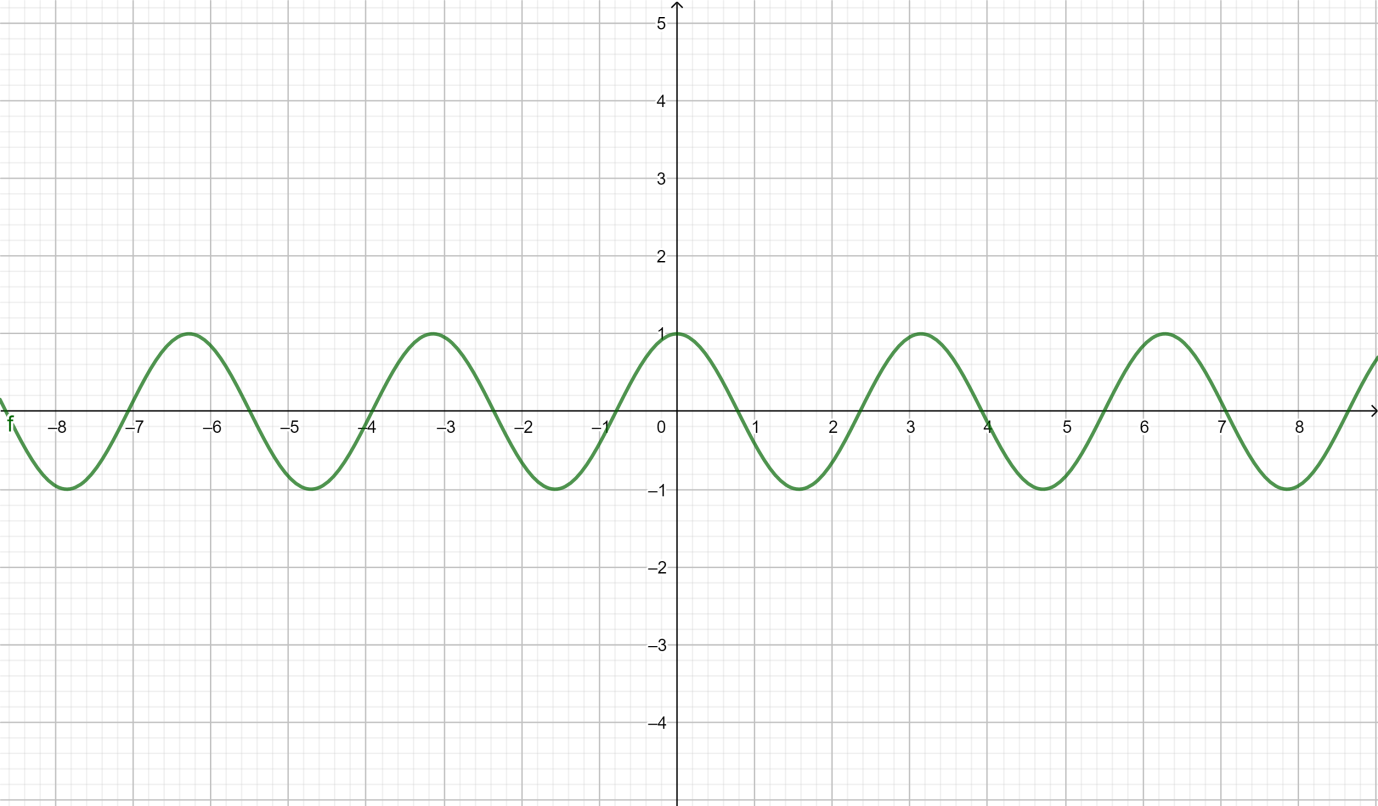
Note: The period of a periodic function is the interval of $x$-values on which the cycle of the graph that is repeated in both directions lies. Therefore, in the case of basic cosine function, $f\left( x \right) = \cos x$ the period is $2\pi$. And the period of $\cos x$ is $2\pi$ so $\cos 2x$ has period $\pi$ and this is also the period of $f\left( x \right)$.
$\cos 2x$ is just a double angle trigonometric function and which tells us that $\cos 2x$Is always equal to${\cos ^2}x - {\sin ^2}x$. The graph of $y = A\cos Bx$ has a property amplitude$= \left| A \right|$, period$= \dfrac{{2\pi }}{B}$. In this problem we have given $y = \cos \left( {2x} \right)$, here Amplitude$= \left| A \right| = 1$ and period$= \dfrac{{2\pi }}{2} = \pi$.