Question

How do you graph $y = - \cos 2x$

Answer 1

We are given a function of cosine that we have to plot on the graph. We have to first convert the
given function to its standard form and then compare it with the standard equation for plotting any
function on the graph, this way we can find out that how the graph of the given function should be
plotted. The standard form of the cosine equation is $y = A\cos (Bx + C) + D$ .

Complete step by step answer:
Comparing $y = - \cos 2x$ with the standard form $y = A\cos (Bx + C) + D$ , we get –
$A = - 1,\,B = 2,\,C = 0\,and\,D = 0$
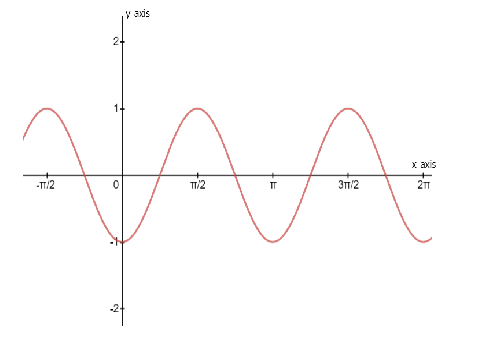
Thus, the given sine function has peak values at -1 and 1, that is, it oscillates between -1 and 1 and
the given cosine function completes two oscillations between 0 and $2\pi$ , but for plotting the
graph, we have to find out the period of the function. Period of this cosine function is –
$p = \dfrac{{2\pi }}{B} \\\ \Rightarrow p = \dfrac{{2\pi }}{2} = \pi \\\$
That is after every $\pi$ radians the given function repeats the oscillation; it completes 1 oscillation
in the interval 0 to $\pi$ .

Note: We know that the general form of the cosine function is $y = A\cos (Bx + C) + D$ where A is the amplitude, the peak values of a function are known as its amplitude. B is the frequency, the number of oscillations that a function does in a fixed interval is known as its frequency. C and D tell us the horizontal and vertical shift of a function respectively. There is no horizontal or vertical shift in the given function as the value of C and D is zero for the given function.