Question

How do you graph $y = 4x + 1$ using slope and intercept?

Answer 1

The slope form of the equation for the straight line is written as $y = mx + c$, where ‘m’ represents the slope of the equation and ‘c’ represents the y-intercept of the line. Now compare the given equation with the standard form and find the intercepts and slope of the line. Intercept is the point where the line meets the coordinate axis.

Complete step by step solution:
Here in this problem, we are given an equation $y = 4x + 1$ , which represents a straight line. And we need to graph this equation in the Cartesian plane using the slope and intercepts of this line.
Before starting with the solution we must understand a few concepts about the straight lines, slopes, and intercepts. A line is a continuous collection of points which does not have any thickness but is infinitely long with no curves. In mathematics, the slope or gradient of a line is a number that describes both the direction and the steepness of the line. The point where the line or curve crosses the axis of the graph is called intercept. If a point crosses the x-axis, then it is called the x-intercept. If a point crosses the y-axis, then it is called the y-intercept.
The slope form of an equation of a straight line is written as:
$\Rightarrow y = mx + c$ , where $'m'$ is the slope of the line and $'c'$ is the y-intercept
Now let’s compare the given equation, i.e. $y = 4x + 1$ with $y = mx + c$ , we get:
$\Rightarrow m = 4{\text{ and }}c = 1$
This implies that the slope of the given equation is $4$ and the y-intercept is of length $1$ or the line intersects with the y-axis at the point $\left( {0,1} \right)$
Now let’s find at what point this line meets the x-axis. This can be done by putting $y = 0$ and then finding the value of $x$ from the equation.
$\Rightarrow {\text{For }}y = 0,{\text{ }}y = 4x + 1 \Rightarrow 0 = 4x + 1 \Rightarrow x = \dfrac{{ - 1}}{4}$
Therefore, the line must be passing through point $\left( { - \dfrac{1}{4},0} \right)$
So now we can mark two points $M\left( {0,1} \right){\text{ and }}N\left( { - \dfrac{1}{4},0} \right)$ on the coordinate plane and then join these two points to form a straight line.
The following figure represents the graph of the line $y = 4x + 1$

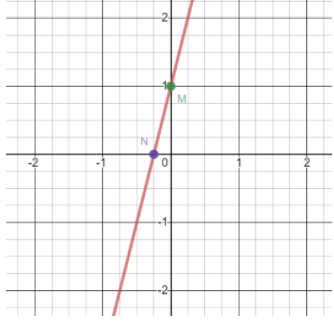
Therefore, we get the graph of the required equation.

Note:
In questions like this, the knowledge of equations of different curves can play a crucial role in solving problems. An alternative approach can be to find any three points on the line and graph a line passing through it. This can be done by hit and trial method.