Question

How do you graph $y=4\csc 2x$?

Answer 1

First compare the function $y=4\csc 2x$ with the base function. Find the period and frequency of the function. Then take some different ‘y’ values for corresponding ‘x’ values and plot the graph.

Complete step-by-step solution:
$y=4\csc 2x$ is a trigonometric function of the base function $y=\csc x$.
As we know $\csc x$ is the reciprocal of $\sin x$, so $\csc x$ will not be defined at the points where $\sin x$ is 0. Hence, the domain of $\csc x$ will be $R-n\pi$, where ‘R’ is the set of real numbers and ‘n’ is an Integers. Similarly, the range of cosec x will be $R-\left( -1,1 \right)$. Since, $\sin x$ lies between $\left( -1,1 \right)$, so $\csc x$ can never lie in the region of $\left( -1,1 \right)$.
Now, considering our equation $y=4\csc 2x$
Here the range of the function will be 4 times from that of $y=\csc x$
Again as we know the period of $\csc x=2\pi$, so the period of $y=4\csc 2x$ will be$=\dfrac{2\pi }{\left| 2 \right|}=\pi$
And the frequency$=\dfrac{1}{\pi }$ (as frequency is the reciprocal of time period)
For the graph we have to take some different values of ‘y’ for corresponding ‘x’ values

x	$\dfrac{\pi }{4}$	$\dfrac{3\pi }{4}$	$\dfrac{5\pi }{4}$	$\dfrac{7\pi }{4}$	$\dfrac{9\pi }{4}$
y	4	$-4$	4	$-4$	4

Taking these values of ‘x’ and ‘y’ the graph can be drawn as

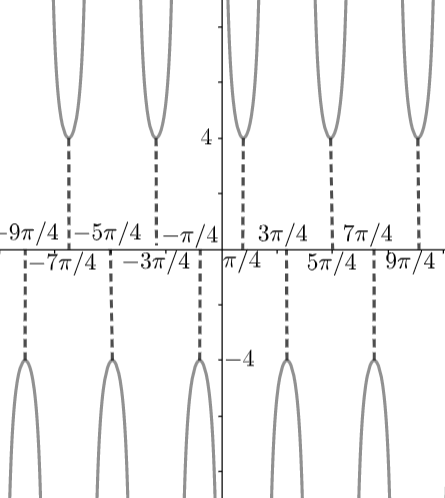
Note: The base function of $y=4\csc 2x$ is $y=\csc x$. From the above graph, we can conclude that the graph of the function $\csc x$ does not have a maximum or a minimum value. The function goes to infinity periodically and is symmetric with the origin.