Question
Question: How do you graph \[y = 3{\left( {x + 3} \right)^2} - 3\] ?...
How do you graph y=3(x+3)2−3 ?
Solution
Hint : Here in this question, we have to plot a graph for the given equation. The given equation resembles or recognised as the standard equation for a parabola, which is f(x)=a(x−h)2+k , where (h,k) is the vertex of the parabola and next find the focus, directrix and the points to plot the required graph.
Complete step-by-step answer :
We know, in the quadratic equation f(x)=ax2+bx+c , a b and c are the constants and x is the variable. So, by finding the different values of x and corresponding values of y or f(x) , we can plot all the points in the graph and by joining all of them we can get the required shape.
here Parabola Formula for the equation of a parabola given in its standard form f(x)=ax2+bx+c is:
Vertex of Parabola = (2a−b,4a4ac−b2)
Focus of the parabola = (2a−b,4a4ac−b2+1)
Directrix of parabola y=4a4ac−b2−1
Now Consider, the given equation
⇒y=3(x+3)2−3
On expanding (x+3)2 using identities (a+b)2=a2+b2+2ab
⇒y=3(x2+32+2(x)(3))−3
⇒y=3(x2+9+6x)−3
⇒y=3x2+27+18x−3
On simplification, we get
⇒y=3x2+18x+24
Where, a=3 , b=18 and c=24
Vertex of Parabola = (2a−b,4a4ac−b2)
⇒(2(3)−18,4(3)4(3)(24)−(18)2)
⇒(6−18,12288−324)
⇒(−3,−3)
Vertex = (−3,−3)
Focus of the parabola = (2a−b,4a4ac−b2+1)
⇒(2(3)−18,4(3)4(3)(24)−(18)2+1)
⇒(6−18,12288−324+1)
⇒(6−18,12−36+1)
⇒(6−18,12−35)
Focus = (6−18,12−35)
Directrix of parabola y=4a4ac−b2−1
⇒4(3)4(3)(24)−(18)2−1
⇒12288−324−1
⇒12−36−1
⇒12−37
Directrix y=12−37
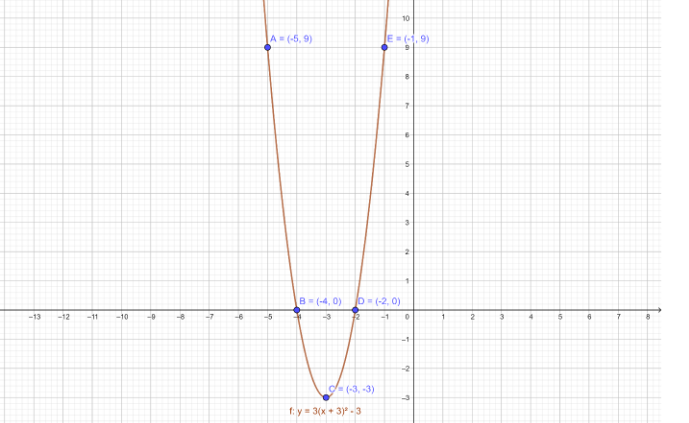
Now putting in different values for x in the equation y=3(x+3)2−3 and calculate the corresponding values for y.
When x=−5⇒y=3(−5+3)2−3⇒y=9
When x=−4⇒y=3(−4+3)2−3⇒y=0
When x=−3⇒y=3(−3+3)2−3⇒y=−3
When x=−2⇒y=3(−2+3)2−3⇒y=0
When x=−1⇒y=3(−1+3)2−3⇒y=9
| x | −5 | −4 | −3 | −2 | −1 |
|---|---|---|---|---|---|
| y | 9 | 0 | −3 | 0 | 9 |
| (x,y) | (−5,9) | (−4,0) | (−3,−3) | (−2,0) | (−1,9) |
Now, plot the required graph:
we determine the values and finally we obtain the linear equation for y and hence we can plot the graph.
Note : The plotting of a graph is different here. When we plot the graph for the parabola we use different methods. Here in this question Vertex of Parabola = (2a−b,4a4ac−b2) , Focus of the parabola = (2a−b,4a4ac−b2+1) , Directrix of parabola y=4a4ac−b2−1
