Question

How do you graph $y = - 2x - 4$ ?

Answer 1

The given equation is an equation of straight line. To graph $y = - 2x - 4$ using slope and $y$-intercept, we must know the general equation of straight line. The general equation of straight line is $y = mx + c$ where $m$ is the slope and $c$ is $y$-intercept. By comparing the given equation with $y = mx + c$, we can find the values of $m$ and $c$. Using these values, we will draw the graph of the given equation.

Complete step-by-step answer:
Here the given equation is $y = - 2x - 4 \cdots \cdots \left( 1 \right)$. We know that the general equation of the straight line is given by $y = mx + c \cdots \cdots \left( 2 \right)$ where $m$ is the slope and $c$ is $y$-intercept. The equation $\left( 2 \right)$ is also called slope-intercept form of straight line.
Let us compare the equation $\left( 1 \right)$ with the equation $\left( 2 \right)$. So, we can write the slope is $m = - 2$ (coefficient of $x$) and $y$-intercept is $c = - 4$. Note that here $y$-intercept is $c = - 4$ so we can say that the straight line is passing through the point $\left( {0, - 4} \right)$. Also note that here slope is $m = - 2$ so we can say that if there is change of two units in $x$ then there will be change of two units in $y$.
Let us find $x$-intercept by putting $y = 0$ in the equation $\left( 1 \right)$. Hence, we get $x = - 2$. Note that here $x$-intercept is $- 2$ so we can say that the straight line is passing through the point $\left( { - 2,0} \right)$.
Now we have the following information:
$\left( 1 \right)$ The required straight line is passing through the points $\left( {0, - 4} \right)$ and $\left( { - 2,0} \right)$.
$\left( 2 \right)$ The slope of the required line is $m = - 2$.
As per the above information, we can draw the graph of the given equation in the following manner.

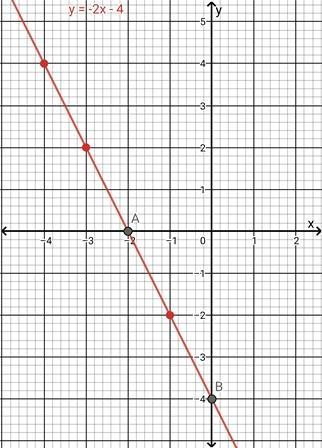
Note:
Rewrite the given equation as $x = - \dfrac{1}{2}y - 2$ and compare with the general equation $x = my + c$, we get $m = - \dfrac{1}{2}$ and $c = - 2$. Here $m = - \dfrac{1}{2}$ is slope and $c = - 2$ is $x$-intercept. To obtain $x$-intercept, we have to put $y = 0$ in the given equation. To obtain $y$-intercept, we have to put $x = 0$ in the given equation. To graph $y = - 2x - 4$, we can use the other method in which first we will find points by putting different values of $x$. Then, by joining all those points we can get the graph of the given equation.