Question

How do you graph $y = 2{x^2} + x - 3$ by plotting points?

Answer 1

Here we will first identify the shape of the graph represented by the given equation. Since the given equation is linear with respect to $y$ and quadratic with respect to $x$, so the given equation represents a parabola. Then, we will convert the equation in the form of the standard equation of parabola. Then we will substitute $X = 0$ and $Y = 0$ to get the coordinates of the vertex. Using these coordinates we will draw the required graph.

Complete step-by-step solution:
According to the question, we have to graph the equation which is given as
$y = 2{x^2} + x - 3$………………….$\left( 1 \right)$
Since the above equation is linear with respect to $y$ and quadratic with respect to $x$, so the given equation represents a parabola whose axis is parallel to the $y$-axis.
Since it represents a parabola, so we will convert it in the standard form of parabola
Taking $2$ common, we have
$y = 2\left( {{x^2} + \dfrac{x}{2} - \dfrac{3}{2}} \right)$
Dividing both the sides by $2$ we get
$\Rightarrow \dfrac{y}{2} = {x^2} + \dfrac{x}{2} - \dfrac{3}{2}$
Multiplying and dividing the middle term by $2$, we have
$\Rightarrow \dfrac{y}{2} = {x^2} + \dfrac{{2x}}{{2 \times 2}} - \dfrac{3}{2}$
$\Rightarrow \dfrac{y}{2} = {x^2} + 2\left( x \right)\left( {\dfrac{1}{4}} \right) - \dfrac{3}{2}$
Adding and subtracting ${\left( {\dfrac{1}{4}} \right)^2}$on the RHS, we have
$\Rightarrow \dfrac{y}{2} = {x^2} + 2\left( x \right)\left( {\dfrac{1}{4}} \right) - \dfrac{3}{2} + {\left( {\dfrac{1}{4}} \right)^2} - {\left( {\dfrac{1}{4}} \right)^2}$
$\Rightarrow \dfrac{y}{2} = {x^2} + 2\left( x \right)\left( {\dfrac{1}{4}} \right) + {\left( {\dfrac{1}{4}} \right)^2} - \dfrac{3}{2} - \dfrac{1}{{16}}$
Now, we know that ${a^2} + 2ab + {b^2} = {\left( {a + b} \right)^2}$. So the above equation can be written as
$\Rightarrow \dfrac{y}{2} = {\left( {x + \dfrac{1}{4}} \right)^2} - \dfrac{3}{2} - \dfrac{1}{{16}}$
$\Rightarrow \dfrac{y}{2} = {\left( {x + \dfrac{1}{4}} \right)^2} - \dfrac{{25}}{{16}}$
Adding $\dfrac{{25}}{{16}}$ on both the sides, we get
$\Rightarrow \dfrac{y}{2} + \dfrac{{25}}{{16}} = {\left( {x + \dfrac{1}{4}} \right)^2}$
$\Rightarrow \dfrac{{8y + 25}}{{16}} = {\left( {x + \dfrac{1}{4}} \right)^2}$
Taking $\dfrac{8}{{16}}$ common on the LHS, we get
$\Rightarrow \dfrac{8}{{16}}\left( {y + \dfrac{{25}}{8}} \right) = {\left( {x + \dfrac{1}{4}} \right)^2}$
$\Rightarrow \dfrac{1}{2}\left( {y + \dfrac{{25}}{8}} \right) = {\left( {x + \dfrac{1}{4}} \right)^2}$
OR
$\Rightarrow {\left( {x + \dfrac{1}{4}} \right)^2} = \dfrac{1}{2}\left( {y + \dfrac{{25}}{8}} \right)$
Now, comparing the above equation with the standard equation of a parabola ${X^2} = kY$, we get
$X = \left( {x + \dfrac{1}{4}} \right)$, $Y = \left( {y + \dfrac{{25}}{8}} \right)$ and $k = \dfrac{1}{2}$
Now, we know that the vertex is determined by putting $X = 0$ and $Y = 0$. Therefore, putting $X = 0$ we have
$\begin{array}{l}x + \dfrac{1}{4} = 0\\\ \Rightarrow x = - \dfrac{1}{4} = - 0.25\end{array}$
Now, we put $Y = 0$ to get
$\begin{array}{l}y + \dfrac{{25}}{8} = 0\\\ \Rightarrow y = - \dfrac{{25}}{8} = - 3.125\end{array}$
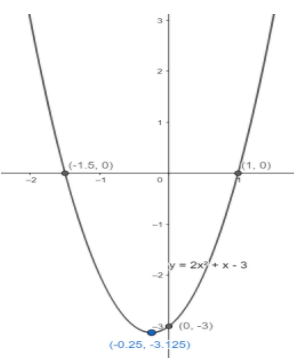
Therefore, the vertex of the parabola is at $\left( { - 0.25, - 3.125} \right)$.
The axis of a parabola passes through its vertex. Since the axis of this parabola is parallel to the y-axis, so the axis is a vertical line cutting the x-axis at $\left( { - 0.25,0} \right)$.
The intersection with the x-axis is found out by putting $y = 0$ in the equation (1) as
$2{x^2} + x - 3 = 0$
Splitting the middle term, we get
$\Rightarrow 2{x^2} - 2x + 3x - 3 = 0$
Factoring out common terms, we get
$\begin{array}{l} \Rightarrow 2x\left( {x - 1} \right) + 3\left( {x - 1} \right) = 0\\\ \Rightarrow \left( {2x + 3} \right)\left( {x - 1} \right) = 0\end{array}$
Applying zero product property, we get
$\begin{array}{l} \Rightarrow \left( {2x + 3} \right) = 0\\\ \Rightarrow x = - \dfrac{3}{2} = - 1.5\end{array}$
Or
$\begin{array}{l} \Rightarrow \left( {x - 1} \right) = 0\\\ \Rightarrow x = 1\end{array}$
Therefore, we get $x = - 1.5,x = 1$.
Therefore, $\left( { - 1.5,0} \right)$ and $\left( {1,0} \right)$ are the points of intersection with the x-axis.
Now, for the intersection with the $y$-axis we put $x = 0$ in the equation $\left( 1 \right)$ to get
$\begin{array}{l}y = 2{\left( 0 \right)^2} + \left( 0 \right) - 3\\\ \Rightarrow y = - 3\end{array}$
Therefore, $\left( {0, - 3} \right)$ is the point of intersection with the y-axis.
Also, the sign of the constant $k$ decides the direction of its opening.
Since $k = \dfrac{1}{2} > 0$, the parabola must be opening upwards.
Hence, the graph of the given equation $y = 2{x^2} + x - 3$ can be drawn as

Note:
The coordinates of the vertex can also be determined by putting the derivative of $y = 2{x^2} + x - 3$ equal to zero. Also, the coefficient of ${x^2}$ can decide the opening side of the parabola. In this case it is equal to $2$ which is greater than zero, which confirms it is opening upwards. If the coefficient of ${x^2}$ is less than 0, then the curve of the parabola opens in downward direction. Here we have used the zero product property to find the values of coordinate. Zero product property states that if the product of two terms is equal to zero, then either of the terms is zero.