Question

How do you graph $y = - 2\sin 2x$?

Answer 1

First find amplitude, period, phase shift, and vertical shift for given periodic function. Select a few points to graph. Find the points at $x = 0$, $x = \dfrac{\pi }{4}$, $x = \dfrac{\pi }{2}$, $x = \dfrac{{3\pi }}{4}$, $x = \pi$. List the points in a table. Then graph the trigonometric function using the amplitude, period, phase shift, vertical shift and the points.

Formula used:
For the graph of $y = a\sin \left( {bx - c} \right) + d$
Amplitude$= \left| a \right|$
Period$= \dfrac{{2\pi }}{{\left| b \right|}}$
Phase Shift$= \dfrac{c}{b}$
Vertical Shift$= d$

Complete step by step solution:
We will use the form $a\sin \left( {bx - c} \right) + d$ to find the amplitude, period, phase shift, and vertical shift.
Compare the given equation $y = - 2\sin 2x$ with $a\sin \left( {bx - c} \right) + d$ and find variables $a,b,c$ and $d$.
$a = - 2$, $b = 2$, $c = 0$ and $d = 0$.
Find the amplitude $\left| a \right|$.
Here, $a = - 2$.
Amplitude, $\left| a \right| = 2$.
Now, find the period using the formula $\dfrac{{2\pi }}{{\left| b \right|}}$.
So, we will calculate the period of the function using $\dfrac{{2\pi }}{{\left| b \right|}}$.
Period: $\dfrac{{2\pi }}{{\left| b \right|}}$
Replace $b$ with $1$ in the formula for period.
Period: $\dfrac{{2\pi }}{{\left| 2 \right|}}$
Solve the equation.
Here, we can observe that the absolute value is the distance between a number and zero.
The distance between $0$ and $2$ is $2$.
Period: $\dfrac{{2\pi }}{2}$
Divide $2\pi$ by $2$.
Period: $\pi$
Now, we will find the phase shift using the formula $\dfrac{c}{b}$.
So, we will calculate the phase shift of the function from $\dfrac{c}{b}$.
Phase Shift: $\dfrac{c}{b}$
Here, replace the values of $c$ and $b$ in the equation for phase shift.
Phase Shift: $\dfrac{0}{2}$
Divide $0$ by $2$.
Phase Shift: $0$
Find the vertical shift $d$.
Vertical Shift: $0$
List the properties of the trigonometric function.
Amplitude: $2$
Period: $\pi$
Phase Shift: $0$($0$ to the left)
Vertical Shift: $0$
Select a few points to graph.
Find the point at $x = 0$.
Replace the variable $x$ with $0$ in the expression.
$f\left( 0 \right) = - 2\sin \left( 0 \right)$
Simplify the result.
The exact value of $\sin \left( 0 \right)$ is $0$.
$f\left( 0 \right) = - 2 \times 0$
Multiply $- 2$ with $0$.
$f\left( 0 \right) = 0$
The final answer is $0$.
Find the point at $x = \dfrac{\pi }{4}$.
Replace the variable $x$ with $\dfrac{\pi }{4}$ in the expression.
$f\left( {\dfrac{\pi }{4}} \right) = - 2\sin \left( {2 \times \dfrac{\pi }{4}} \right)$
Simplify the result.
The exact value of $\sin \left( {\dfrac{\pi }{2}} \right)$ is $1$.
$f\left( {\dfrac{\pi }{4}} \right) = - 2$
The final answer is $- 2$.
Find the point at $x = \dfrac{\pi }{2}$.
Replace the variable $x$ with $\dfrac{\pi }{2}$ in the expression.
$f\left( {\dfrac{\pi }{2}} \right) = - 2\sin \left( {2 \times \dfrac{\pi }{2}} \right)$
Simplify the result.
The exact value of $\sin \left( \pi \right)$ is $0$.
$f\left( {\dfrac{\pi }{2}} \right) = 0$
The final answer is $0$.
Find the point at $x = \dfrac{{3\pi }}{4}$.
Replace the variable $x$ with $\dfrac{{3\pi }}{4}$ in the expression.
$f\left( {\dfrac{{3\pi }}{4}} \right) = - 2\sin \left( {2 \times \dfrac{{3\pi }}{4}} \right)$
Simplify the result.
The exact value of $\sin \left( {\dfrac{{3\pi }}{2}} \right)$ is $- 1$.
$f\left( {\dfrac{{3\pi }}{4}} \right) = 2$
The final answer is $2$.
Find the point at $x = \pi$.
Replace the variable $x$ with $\pi$ in the expression.
$f\left( \pi \right) = - 2\sin \left( {2\pi } \right)$
Simplify the result.
The exact value of $\sin \left( {2\pi } \right)$ is $0$.
$f\left( \pi \right) = - 2 \times 0$
Multiply $- 2$ with $0$.
$f\left( \pi \right) = 0$
The final answer is $0$.
List the points in a table.

$x$	$f\left( x \right)$
$0$	$0$
$\dfrac{\pi }{4}$	$- 2$
$\dfrac{\pi }{2}$	$0$
$\dfrac{{3\pi }}{4}$	$2$
$\pi$	$0$

The trigonometric function can be graphed using the amplitude, period, phase shift, vertical shift and the points.
Amplitude: $2$
Period: $\pi$
Phase Shift: $0$($0$ to the left)
Vertical Shift: $0$

$x$	$f\left( x \right)$
$0$	$0$
$\dfrac{\pi }{4}$	$- 2$
$\dfrac{\pi }{2}$	$0$
$\dfrac{{3\pi }}{4}$	$2$
$\pi$	$0$

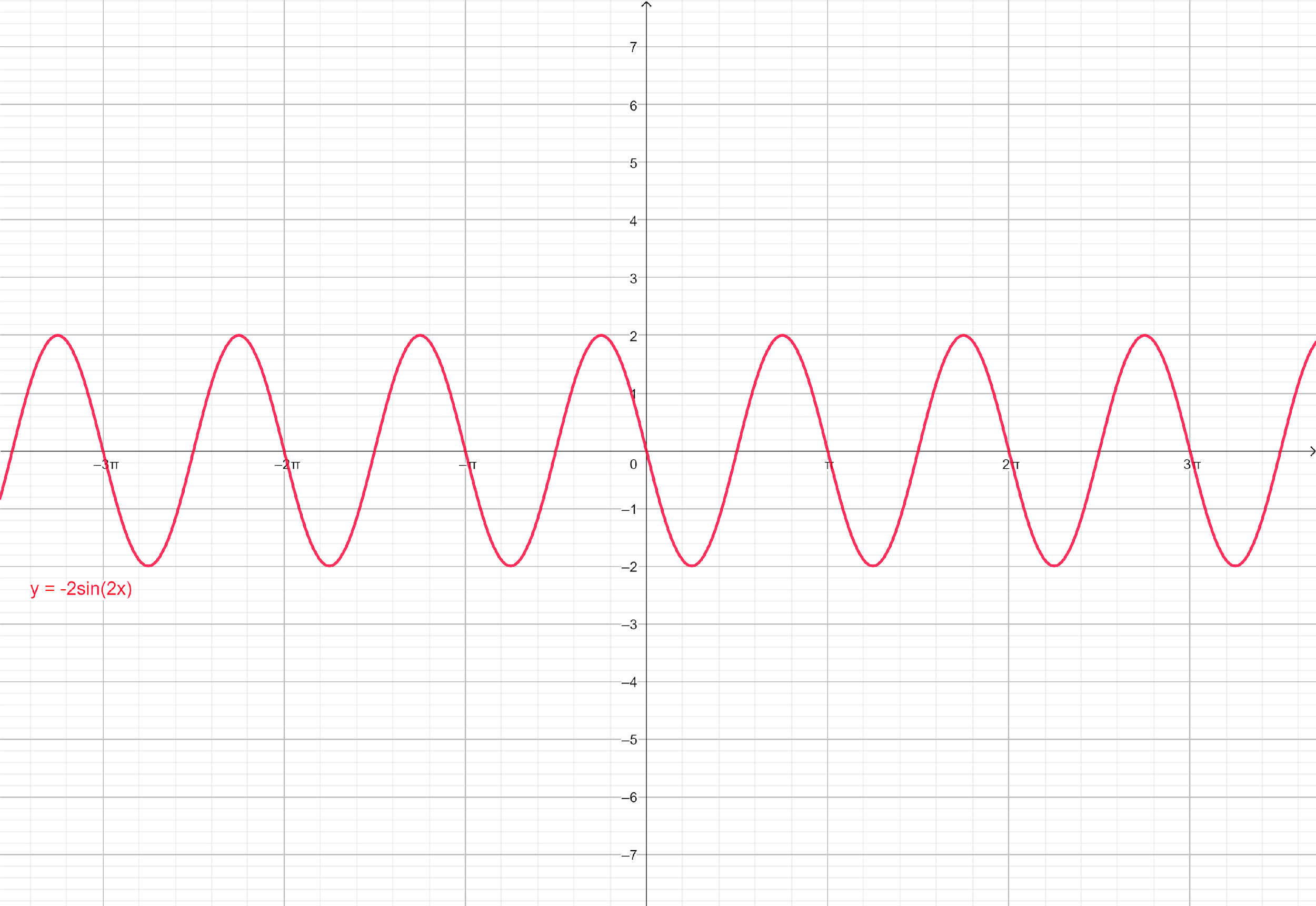
Note: $2\sin 2x$ and $2\sin x$ are entirely different terms.
$2\sin x$ is double the sine function of angle $x$. It lies between $- 2$ and $2$.
$2\sin 2x$ is twice the sine of angle $2x$. It is $2$ times the angle $x$. The value of $2\sin 2x$ is between $- 2$ and $2$.