Question

How do you graph $y = - 2{\left( {x - 2} \right)^2} - 4$?

Answer 1

We are given equation and we have to find how to graph that equation. The given equation is of parabola and we have to graph that parabola for that first we will identify the vertex as we have our parabola in the vertex form, which makes the process very easy. For parabola in vertex form we will use:
Y=a(x-h) +k
Here the vertex is (h, k). Then we will identify the intercepts. This is x intercepts (where y=0), and y intercepts (where x=0). After finding the intercepts we will identify the direction of parabola. This is pretty straightforward; the direction depends on the sign of a. Value at the front of your equation. If it is negative so it will point downwards and for positive it will point upward. To graph the equation on a graph we will need some easy points. It means we plug in some values of x for which it is pretty straightforward to find the value of y. using the points we will graph that points and graph the equation.

Complete step-by-step answer:
Step1: We are given the equation $y = - 2{\left( {x - 2} \right)^2} - 4$ we will use the vertex form i.e. Y=a(x-h) +k first we will compare the equation from this general equation to find the values of a, h and k. on comparing the values we will get $a = - 2,h = 2,k = - 4$. Since the value of a is negative, the parabola opens down now we will find the vertex i.e. (h, k) so the vertex is $\left( {2, - 4} \right)$. Now we will find the distance from the vertex to a focus of the parabola by using the formula:
$P=\dfrac{1}{4a}$
On substituting the value of a we will get:
$\Rightarrow p = \dfrac{1}{{4 \times 2}}$
$\Rightarrow p = \dfrac{1}{8}$
Step2: Now we will find the focus of a parabola by adding p to the y coordinate k if the parabola opens down. Foci is (h,k+p)
Using the values of h,k,p we will find the focus.
$\Rightarrow \left( {2,\left( { - 4 + \dfrac{1}{8}} \right)} \right)$
$\Rightarrow \left( {2,\dfrac{{ - 31}}{8}} \right)$
Now we will find the axis of symmetry by finding the line that passes through the vertex and the focus we will get:
$x = 2$
Step3: Now we will find the directrix of a parabola by subtracting p from the y-coordinate k of the vertex if the parabola opens down.
y=k-p
Now we will substitute the value of k and p and find the value of y:
$\Rightarrow y = - 4 - \dfrac{1}{8}$
On further solving we will get:
$\Rightarrow y = \dfrac{{ - 33}}{8}$
By using the properties of parabola we have found the values of the following :
Direction : opens down
Vertex :$\left( {2, - 4} \right)$
Focus :$\left( {2,\dfrac{{ - 31}}{8}} \right)$
Axis of symmetry:$x = 2$
Directrix:$y = \dfrac{{ - 33}}{8}$
Step4: Select a few x values and plug them into the equation to find the corresponding y-values. The x-values should be selected around the vertex.
On simplifying the equation it becomes:
$\Rightarrow y = - 2{x^2} + 8x - 12$
On putting $x = 0$ we get:
$\Rightarrow y = - 2{\left( 0 \right)^2} + 8\left( 0 \right) - 12$
$\Rightarrow y = - 12$
Similarly on substituting $x = 1$ we get:
$\Rightarrow y = - 2{\left( 1 \right)^2} + 8\left( 1 \right) - 12$
$\Rightarrow y = - 6$
Substituting $x = 2$ we get:
$\Rightarrow y = - 2{\left( 2 \right)^2} + 8\left( 2 \right) - 12$
$\Rightarrow y = 0$
Now we will make the table for the values of x and y to graph the equation:

x	y
$0$	$- 12$
$1$	$- 6$
$2$	$0$
$3$	$- 6$
$4$	$- 12$

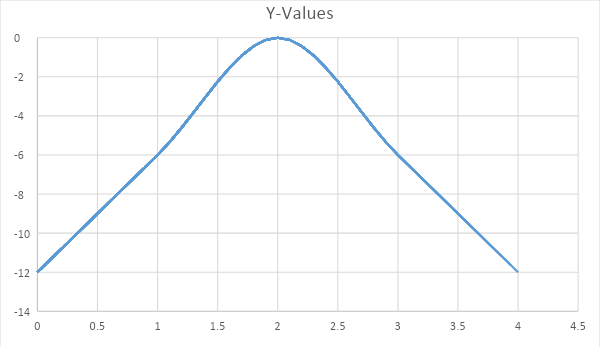
Step5: Final answer: Hence the equation is graphed above

Note:
In this type of questions students mainly make mistakes in identifying vertex or intercept. The sign mistakes also in finding the direction of parabola in which it opens if the sign of a is negative parabola is going to be pointed downward and if it is positive then it will point in upward direction. They make mistakes in graphing the equation. The easy method is to make a chart of x and y and unplug the values of x into the equation to find the value of by and use those coordinates to graph the equation on the graph.