Question

How do you graph $y - 2 = \dfrac{2}{3}\left( {x - 4} \right)$?

Answer 1

The easiest way to find points on the line of the given equation $y - 2 = \dfrac{2}{3}\left( {x - 4} \right)$ is to convert the given equation in point slope form to slope intercept form: $y = mx + b$, where m is the slope, and b is the y-intercept. In order to do this, solve the point slope equation for y, then consider any x values to graph the solution.

Complete step by step solution:
Let us write the given equation:
$y - 2 = \dfrac{2}{3}\left( {x - 4} \right)$
Every straight line can be represented by an equation $y = mx + b$, hence let us apply the slope intercept form to graph the solution.
$y - 2 = \dfrac{2}{3}\left( {x - 4} \right)$
Add 2 on both sides of the given equation as:
$y - 2 + 2 = \dfrac{2}{3}\left( {x - 4} \right) + 2$
\Rightarrow $$$$y = \dfrac{2}{3}\left( {x - 4} \right) + 2
Now let us simplify the obtain equation
$\dfrac{2}{3}\left( {x - 4} \right) + 2$ to $\dfrac{{2\left( {x - 4} \right)}}{3}$
\Rightarrow $$$$y = \dfrac{{2\left( {x - 4} \right)}}{3} + 2
Expand the terms as:
$y = \dfrac{{2x}}{3} - \dfrac{8}{3} + 2$
Now simplify the terms
$y = \dfrac{2}{3}x - \dfrac{8}{3} + 2$
Multiply 2 by $\dfrac{3}{3}$ to get the same denominator as $- \dfrac{8}{3}$ i.e.,
$y = \dfrac{2}{3}x - \dfrac{8}{3} + 2 \times \dfrac{3}{3}$
Simplifying the terms, we get
$y = \dfrac{2}{3}x - \dfrac{8}{3} + \dfrac{6}{3}$
$y = \dfrac{2}{3}x - \dfrac{2}{3}$ ……….. 1
Determine two or three points on the line by choosing values for x and solving for y.
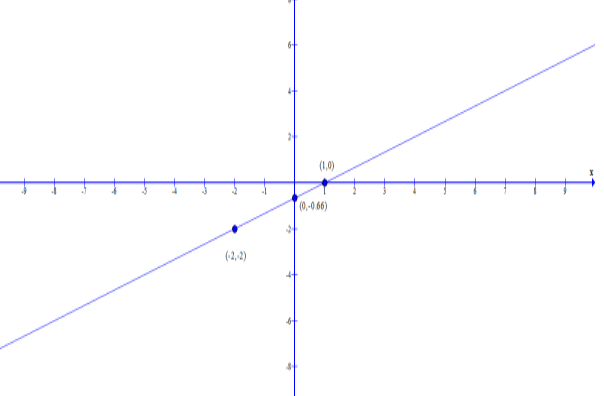
Let us consider the points at x as -2, 0 and 1.
Substitute the values of x in equation 1, hence we get
$x = - 2,y = - 2$
$x = 0,y = - \dfrac{2}{3}$or 0.66
$x = 1,y = 0$
Now, let us graph the solution at $x = - 2,y = - 2$,
$x = 0,y = - \dfrac{2}{3}$ and $x = 1,y = 0$
Plot the points and draw a straight line through them.

Note:
In slope intercept form; very often, linear-equation word problems deal with changes over the course of time i.e., $y = mx + b$ the number b is the coordinate on the y-axis where the graph crosses the y-axis and also, we can solve the given equation using intercept form i.e., when x = 0, the corresponding y-value is the y-intercept. In the particular context of word problems, the y-intercept (that is, the point when x = 0) also refers to the starting value.