Question

How do you graph $x = 7?$

Answer 1

To solve the above question, we need to compare the given equation of the line with the standard equation of a line. On comparing the given equation with the standard equation, we will get the values of the slope and the y-intercept of the given line. From these values, the required graph of the given equation can be easily plotted.

Formula used:
The formula used to solve this question is given by
$y = mx + c$, where $m$ and $c$ are respectively the slopes and the y-intercept of a line.

Complete step by step solution:
We know that the standard equation of a line is given by
$y = mx + c$ ………………..(1)
Also, the equation given in the question is
$x = 7$
Subtracting $x$ from both sides, we get
$0 = 7 - x$
$\Rightarrow 0 = - x + 7$
Multiplying by $- 1$ on both the sides of the above equation, we get
$0 = x - 7$
Writing the above equation in the form of the standard equation of a line, we get
$0\left( y \right) = x - 7$ ………………………………....(2)
On comparing the equations (1) and (2) we get
$m \to \infty$

Thus, the slope of the graph of the given must be infinitely large. This means that the graph must be a vertical line cutting the x-axis at the point $\left( {7,0} \right)$. Hence, the graph of the line $x = 7$ is given as-

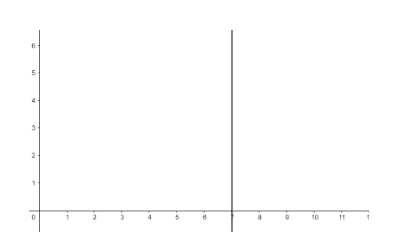
Note:
The coefficient of $y$ in the given equation is equal to zero. So while converting the given equation in the standard form of $y = mx + c$, do not divide the equation by zero, as it is not allowed in mathematics. Also, the slope must not be called to be equal to infinity. The slope in this case is defined only in the limiting sense and is defined to be tending towards infinity.