Question

How do you graph ${x^2} + {y^2} - 6x + 8y + 9 = 0$ ?

Answer 1

Hint : We need to know the standard form of a circle equation to solve this question. This question involves the arithmetic operations like addition/ subtraction/ multiplication/ division. Also, we need to know the basic algebraic formulae to make an easy calculation. We need to know how to draw a graph with the help of a given equation.

Complete step by step solution:
The given equation is shown below,
${x^2} + {y^2} - 6x + 8y + 9 = 0 \to \left( 1 \right)$
We know that,
The standard form of circle equation is,
${\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {r^2} \to \left( 2 \right)$
Here, $\left( {a,b} \right)$ is the centre of the circle,
And $r$ is the radius of the circle.
We would convert the equation $\left( 1 \right)$ into the form of the equation $\left( 2 \right)$ . So, let’s rearrange the equation $\left( 1 \right)$ , as given below,
${x^2} - 6x + {y^2} + 8y = - 9 \to \left( 3 \right)$
( $6x$ Can be written as $2 \times 3 \times x$
$8y$ Can be written as $2 \times 4 \times y$ )
Let’s add ${3^2}$ and ${4^2}$ on both sides of the equation $\left( 3 \right)$ , we get
${x^2} - 6x + {3^2} + {y^2} + 8y + {4^2} = - 9 + {3^2} + {4^2} \to \left( 4 \right)$
We know that,
${\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab$ And
${\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab$
By using the above two algebraic formula, we get
${x^2} - 6x + {3^2} = {\left( {x - 3} \right)^2}$ And
${y^2} + 2y + {4^2} = {\left( {y + 4} \right)^2}$
Let’s substitute the above two equations in the equation $\left( 4 \right)$ , we get
$\left( 4 \right) \to {x^2} - 6x + {3^2} + {y^2} + 8y + {4^2} = - 9 + {3^2} + {4^2}$
${\left( {x - 3} \right)^2} + {\left( {y + 4} \right)^2} = - 9 + 9 + {4^2}$
So, we get
${\left( {x - 3} \right)^2} + {\left( {y + 4} \right)^2} = {4^2} \to \left( 5 \right)$
Let’s compare the equation $\left( 2 \right)$ and $\left( 5 \right)$ , we get
$\left( 2 \right) \to {\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {r^2}$
$\left( 5 \right) \to {\left( {x - 3} \right)^2} + {\left( {y + 4} \right)^2} = {4^2}$
So, we get $a = 3,b = - 4$ and $r = 4$
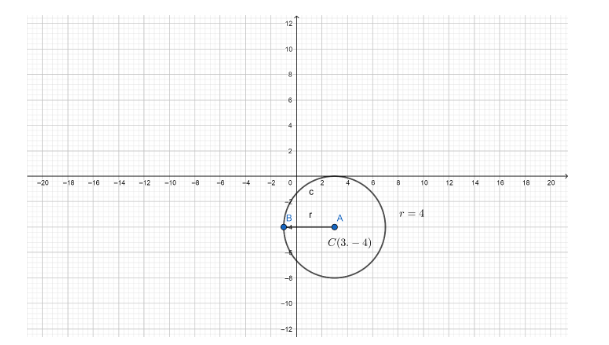
So, the centre $\left( {a,b} \right) = \left( {3, - 4} \right)$ and the radius $r = 4$
By using the above information we can draw the following graph,
The above graph has defined the equation,
${x^2} + {y^2} - 6x + 8y + 9 = 0$

Note : Remember the standard form of the circle equation. Also, note that for making the given equation to algebraic formulae we can add/ subtract/ multiply/ divide any number with the equation into both sides. Also, note that in the equation ${\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {r^2}$ , the centre of the circle is mentioned as $\left( {a,b} \right)$ and the radius of the circle is mentioned as $r$ .