Question

How do you graph ${x^2} + {y^2} + 6x - 8y + 9 = 0$

Answer 1

Given a polynomial and we have to plot a graph of the polynomial. To plot the graph of the polynomial, first, we will rewrite the equation in the form of the standard equation of the circle. Then determine the coordinates for the centre of the circle, and the radius of the circle. Then draw the circle using the centre and the radius.

Formula used:
The formula for the binomial ${\left( {a \pm b} \right)^2}$ is given as:
${a^2} \pm 2ab + {b^2}$
The standard equation of the circle is given as:
${\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {r^2}$
Where $a$ and $b$ are the coordinates of the centre and $r$ is the radius of the circle

Complete step-by-step answer:
We are given the polynomial ${x^2} + {y^2} + 6x - 8y + 9 = 0$. First rewrite the equation by arranging $x$ and $y$ terms together.
$\left( {{x^2} + 6x} \right) + \left( {{y^2} - 8y} \right) + 9 = 0$
Now, we will move the constant term on the right hand side of the equation.
$\left( {{x^2} + 6x} \right) + \left( {{y^2} - 8y} \right) = - 9$
Now complete the squares by adding ${3^2}$ on both sides and ${4^2}$ on both sides of the equation.
$\left( {{x^2} + 6x + {3^2}} \right) + \left( {{y^2} - 8y + {4^2}} \right) = - 9 + {3^2} + {4^2}$
$\left( {{x^2} + 6x + 9} \right) + \left( {{y^2} - 8y + 16} \right) = - 9 + 9 + {4^2}$
Now we will apply the formula for squared binomials to the LHS of the equation.
${\left( {x + 3} \right)^2} + {\left( {y - 4} \right)^2} = - 9 + 9 + {4^2}$
On simplifying the terms on the RHS of the equation, we get:
${\left( {x + 3} \right)^2} + {\left( {y - 4} \right)^2} = {4^2}$
Now, we will compare the equation with the standard equation of the circle to determine the value of $a$, $b$ and $r$.
$\Rightarrow a = - 3$
$\Rightarrow b = 4$
$\Rightarrow r = 4$
Thus, the coordinates for the centre of the circle is $\left( { - 3,4} \right)$ and radius of the circle is $4$ units.
Now we will draw the circle with centre $\left( { - 3,4} \right)$ and $r = 4$.

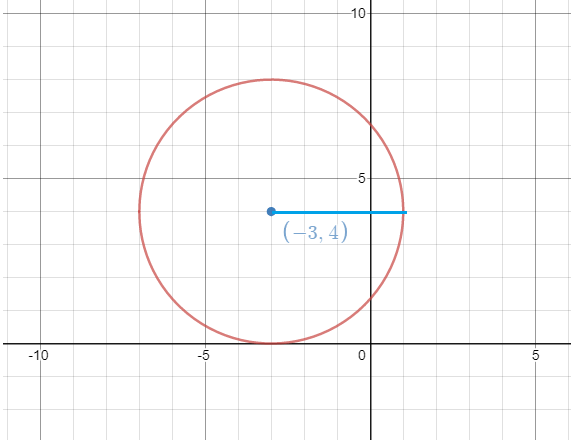
Final answer: Hence the graph of the polynomial is

Note:
In such types of questions students mainly make mistakes while plotting the points on the set of axes. In an ordered pair $\left( {x,y} \right)$, the value of $x$ is the distance of the point from $y$-axis whereas the value of $y$ is plotted by taking the distance from the $x$-axis. In such types of questions, the graph of the circle is obtained by plotting the coordinates of the centre and taking the radius of desired units.