Solveeit Logo
Login

Question

Question: How do you graph \({x^2} + {y^2} - 6x + 2y - 6 = 0\)?...

How do you graph x2+y2−6x+2y−6=0{x^2} + {y^2} - 6x + 2y - 6 = 0?

Explanation

Solution

We will first use the method of completing the square and rewrite the given equation. Now, we will compare it to the general equation of a circle and draw it using radius and circle.

Complete step-by-step answer:
We are given that we are required to graph x2+y2−6x+2y−6=0{x^2} + {y^2} - 6x + 2y - 6 = 0.
We can write this given equation as:-
⇒x2−2×3×x+y2+2×y−6=0\Rightarrow {x^2} - 2 \times 3 \times x + {y^2} + 2 \times y - 6 = 0
Adding and subtracting 9 from the above mentioned equation, we will get the following equation:-
⇒x2−6x+9−9+y2+2×y−6=0\Rightarrow {x^2} - 6x + 9 - 9 + {y^2} + 2 \times y - 6 = 0 ………………(1)
Now, we know that we have an identity given by: (a−b)2=a2+b2−2ab{(a - b)^2} = {a^2} + {b^2} - 2ab
Replacing a by x and b by 3, we will then obtain the following equation:-
⇒(x−3)2=x2+32−2×3×x\Rightarrow {(x - 3)^2} = {x^2} + {3^2} - 2 \times 3 \times x
Simplifying the right hand side in the above equation, we will then obtain the following equation:-
⇒(x−3)2=x2+9−6x\Rightarrow {(x - 3)^2} = {x^2} + 9 - 6x
Putting this above mentioned equation in equation number (1), we will then obtain the fact that the given expression can be written as following:-
⇒(x−3)2−9+y2+2×y−6=0\Rightarrow {(x - 3)^2} - 9 + {y^2} + 2 \times y - 6 = 0
Adding and subtracting 1 from the above mentioned equation, we will get the following equation:-
⇒(x−3)2−9+y2+2y+1−1−6=0\Rightarrow {(x - 3)^2} - 9 + {y^2} + 2y + 1 - 1 - 6 = 0 ………………..(2)
Now, we know that we have an identity given by: (a+b)2=a2+b2+2ab{(a + b)^2} = {a^2} + {b^2} + 2ab
Replacing a by y and b by 1, we will then obtain the following equation:-
⇒(y+1)2=y2+12+2×1×y\Rightarrow {(y + 1)^2} = {y^2} + {1^2} + 2 \times 1 \times y
Simplifying the right hand side in the above equation, we will then obtain the following equation:-
⇒(y+1)2=y2+1+2y\Rightarrow {(y + 1)^2} = {y^2} + 1 + 2y
Putting this above mentioned equation in equation number (2), we will then obtain the fact that the given expression can be written as following:-
⇒(x−3)2−9+(y+1)2−6−1=0\Rightarrow {(x - 3)^2} - 9 + {(y + 1)^2} - 6 - 1 = 0
Simplifying the terms out of the bracket and taking them to the right hand side, we will then obtain the following expression:-
⇒(x−3)2+(y+1)2=16\Rightarrow {(x - 3)^2} + {(y + 1)^2} = 16
We can also write this equation as:
⇒(x−3)2+(y+1)2=42\Rightarrow {(x - 3)^2} + {(y + 1)^2} = {4^2}
Now, we have a circle with centre (3, - 1) and radius as 4 units.
Drawing this, we will obtain the following:-

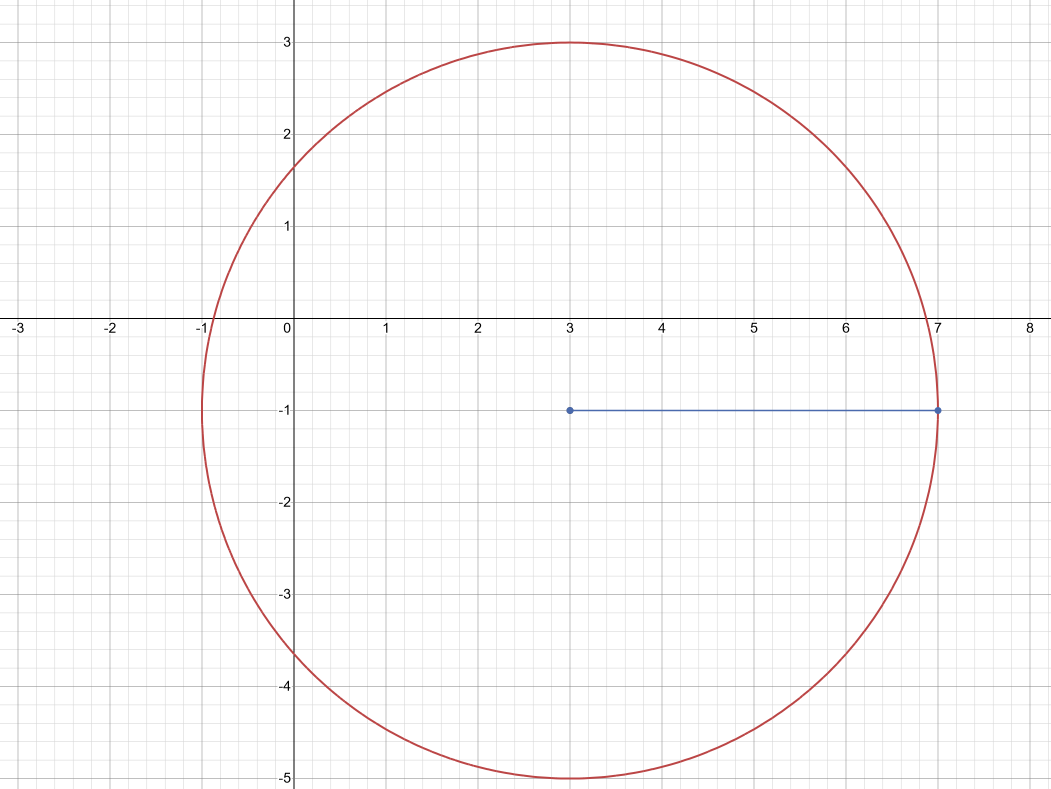
Thus, we have required the graph of the given expression.

Note:
The students must note that while finding the radius and centre of the circle, we used the fact that “The general equation of a circle is given by: (x−h)2+(y−k)2=r2{(x - h)^2} + {(y - k)^2} = {r^2}, where (h, k) is the centre of the circle and r is its radius”.
We compared this to (x−3)2+(y+1)2=42{(x - 3)^2} + {(y + 1)^2} = {4^2} and got the centre as (3, - 1) and the radius as 4 units.