Solveeit Logo
Login

Question

Question: How do you graph \({x^2} + {y^2} - 6x + 2y - 6 = 0\)?...

How do you graph x2+y2−6x+2y−6=0{x^2} + {y^2} - 6x + 2y - 6 = 0?

Explanation

Solution

In this question, we will try to rearrange the terms in the equation and try to get it in the form of a standard circle equation. Then, from that equation, we will take the points of the centre and the radius and using them, we will plot the graph.

Formula used: Standard equation of a circle: (x−a)2+(y−b)2=r2{(x - a)^2} + {(y - b)^2} = {r^2}
Where (a,b)(a,b) is the centre of the circle and rr is the radius of the circle

Complete step by step solution:
We have the equation given as:
x2+y2−6x+2y−6=0{x^2} + {y^2} - 6x + 2y - 6 = 0
Now, on grouping the similar terms and shifting the constant value on the right-hand side, we get:
(x2−6x)+(y2+2y)=6({x^2} - 6x) + ({y^2} + 2y) = 6
Now, to get the equation in the form of a standard circle equation, we will complete the squares by adding numbers on both sides of the equation.
Now the third term should be such that it is the square of the coefficient of xx divided by 22. Therefore, we will add (62)2{\left( {\dfrac{6}{2}} \right)^2} which is 32{3^2} and (22)2{\left( {\dfrac{2}{2}} \right)^2} which is 11 on both the sides of the equation.
On completing the squares, we get:
(x2−6x+32)+(y2+2y+1)=6+32+1({x^2} - 6x + {3^2}) + ({y^2} + 2y + 1) = 6 + {3^2} + 1
We know that(a+b)2=a2+2ab+b2{(a + b)^2} = {a^2} + 2ab + {b^2} . Therefore, on writing the square in the simplified manner, we get:
(x−3)2+(y+1)2=6+9+1=16{(x - 3)^2} + {(y + 1)^2} = 6 + 9 + 1 = 16
Now we know that 42=16{4^2} = 16 therefore, on simplifying the right-hand side we get:
(x−3)2+(y+1)2=42{(x - 3)^2} + {(y + 1)^2} = {4^2}
Now the standard equation of the circle is: (x−a)2+(y−b)2=r2{(x - a)^2} + {(y - b)^2} = {r^2}
Therefore, the above expression can be also being written as:
(x−3)2+(y−(−1))2=42{(x - 3)^2} + {(y - ( - 1))^2} = {4^2}
On comparing the equation with the equation of a standard circle, we get:
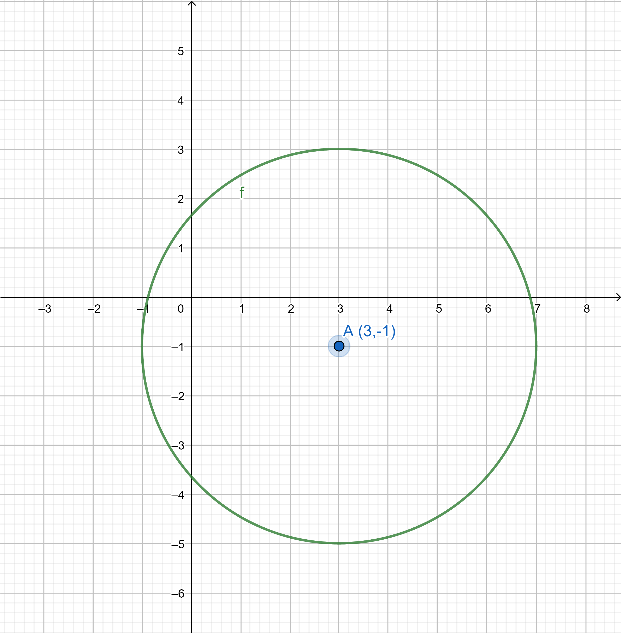
The centre of the circle is (3,−1)(3, - 1) and the radius of the circle is 44.
The circle can be plotted on the graph as:
In this graph, point A is the radius of the circle.

Note: The equation of circle with centre at (0,0)\left( {0,0} \right) will have the equation asx2+y2=r2{x^2} + {y^2} = {r^2} .
Equation of circle in General form: The general equation of the form is – x2+y2+2gx+2fy+c=0{x^2} + {y^2} + 2gx + 2fy + c = 0
In this case, radius of the circle =g2+f2−c = {g^2} + {f^2} - c and centre of the circle=(−g,−f) = \left( { - g, - f} \right)