Question

How do you graph ${x^2} + {y^2} - 4x + 6y - 12 = 0$?

Answer 1

Given an equation. We have to graph the equation. First, rewrite the equation in standard form of the circle equation. Then, determine the points of the centre and the radius of the circle from the equation. Then, we will draw the graph.
The standard form of equation of a circle is given by:
${\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}$
Where $\left( {h,k} \right)$ is the centre of the circle and r is the radius

Complete step by step solution:
We are given an equation, ${x^2} + {y^2} - 4x + 6y - 12 = 0$.

Now, we will group the similar terms on the left hand side of the equation and shift the constant terms on the right hand side.

$\Rightarrow \left( {{x^2} - 4x} \right) + \left( {{y^2} + 6y} \right) = 12$

Now, complete the square to form the equation on left hand side by adding numbers to each group.

Here, the third term added must be square of the coefficient of x divided by 2.

Thus, we will add ${\left( {\dfrac{4}{2}} \right)^2} = 4$ and ${\left( {\dfrac{6}{2}} \right)^2} = 9$ to both sides of the equation.

$\Rightarrow \left( {{x^2} - 4x + 4} \right) + \left( {{y^2} + 6y + 9} \right) = 12 + 4 + 9$

$\Rightarrow \left( {{x^2} - 4x + 4} \right) + \left( {{y^2} + 6y + 9} \right) = 25$

Now, apply the algebraic identity ${\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}$ to the left hand side of the equation.

$\Rightarrow {\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} = {5^2}$

Rewrite the equation in the standard form of equation of circle.

$\Rightarrow {\left( {x - 2} \right)^2} + {\left( {y - \left( { - 3} \right)} \right)^2} = {5^2}$

Now, we will compare the obtained equation by the standard equation of circle.

$\Rightarrow \left( {h,k} \right) = \left( {2, - 3} \right)$

$\Rightarrow r = 5$

Therefore, the centre of the circle is $\left( {2, - 3} \right)$ and radius of the circle is $5$.

Now, we will plot the circle on the graph as:

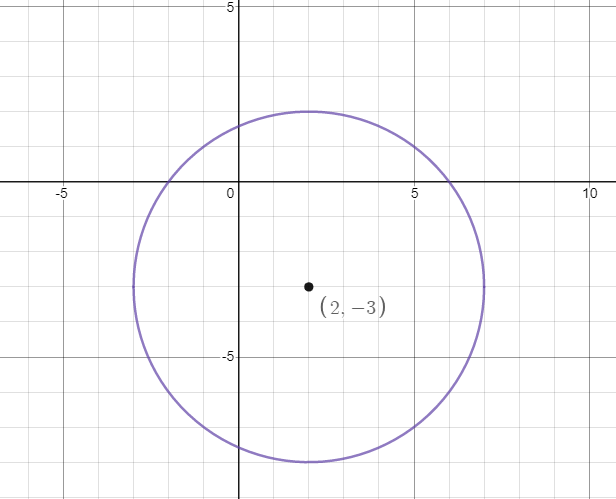
Note: Please note that the equation of the circle whose centre if the origin will have the equation ${x^2} + {y^2} = {r^2}$. Also, the general form of the equation of the circle is ${x^2} + {y^2} + 2gx + 2fy + c = 0$ where the centre is $\left( { - g, - f} \right)$ and the radius of the circle is the square root of ${g^2} + {f^2} - c$