Question

How do you graph ${x^2} + {y^2} = 4$?

Answer 1

For solving this type of question, we will compare the equation with the standard from of equation with the circle that is given by ${\left( {x - m} \right)^2} + {\left( {y - n} \right)^2} = {k^2}$. From there on, solving for the value of K we will get the points which are passing through both the axes.

Complete step-by-step answer:
Here in this problem, we are given an equation of a curve, i.e. ${x^2} + {y^2} = 4$. And we need to graph this curve in the coordinate plane.
Before starting the solution, we must understand a few concepts about the curves. A curve is defined as a smoothly- flowing continuous line that has bent. It does not have any sharp turns. The way to identify the curve is that the line bends and changes its direction at least once. Circles, ellipses, parabolas, and hyperbolas, as well as arcs, sectors, and segments, are two-dimensional curved shapes. Whereas, shapes such as spheres, cylinders, and cones are referred to as three-dimensional curved shapes.
For a circle, having its center at a point with coordinates $\left( {m,n} \right)$ and having a radius of length $'k'{\text{ units}}$ , the equation in the standard form is given as ${\left( {x - m} \right)^2} + {\left( {y - n} \right)^2} = {k^2}$ . In this equation, ‘m’, ‘n’, and ‘k’ are constant with real values and $\left( {x,y} \right)$ represent an arbitrary point in the circle.
So for the given equation ${x^2} + {y^2} = 4$ , we can compare it with the standard form of the equation of the circle, i.e. ${\left( {x - m} \right)^2} + {\left( {y - n} \right)^2} = {k^2}$ , we will get:
$\Rightarrow m = 0,n = 0{\text{ and }}{k^2} = 4$
On solving, we can get the value of ‘k’ as: ${k^2} = 4 \Rightarrow k = \sqrt 4 = 2$
Therefore, the above conclusion implies that the given equation is an equation of the circle which has its center coordinates as $\left( {m,n} \right) = \left( {0,0} \right)$ and is of the radius $k = 2{\text{ units}}$ .
So we can graph this equation by making a circle centered at the origin $\left( {0,0} \right)$ and passing through the x-axis and y-axis through the points $\left( {0,2} \right),\left( {2,0} \right),\left( {0, - 2} \right){\text{ and }}\left( { - 2,0} \right)$
The following figure can represent the above circle:

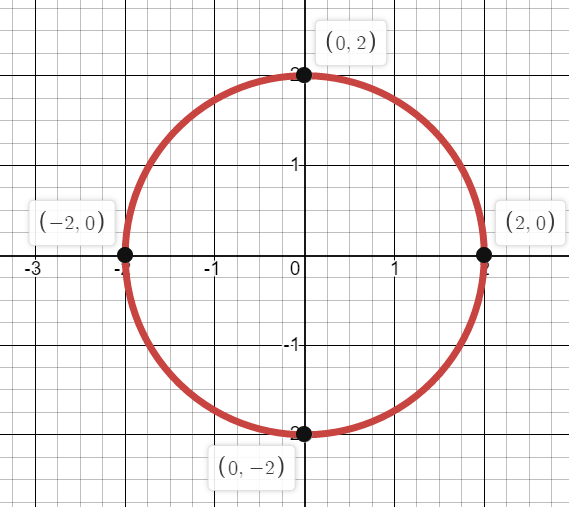
Thus, we get the required graph as a circle as shown in the above figure.

Note: In this question, the use of the standard form of the equation of circle played a crucial role in the solution of the question. An alternative approach can be to use the general form of the equation of a circle, i.e. ${x^2} + {y^2} + 2gx + 2fy + c = 0$ and compare the given equation in the question with it. And thus we get the center as $\left( { - g, - f} \right)$ and the radius as $\sqrt {{g^2} + {f^2} - c}$ .