Question

How do you graph ${x^2} + {y^2} = 36$

Answer 1

Here we use the standard form of a circle that is ${\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {r^2}$ where $\left( {a,b} \right)$ are coordinates of the circle and $r$ is the radius of the circle. By using this standard form of a circle we will have the required result.
Formula used: The equation of a circle is ${\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {r^2}$

Complete step by step answer:
We need to draw the graph of the given equation
So we are proceeding in that way
The given question can be written in the form of the standard form of a circle in the following way:
${\left( {x - 0} \right)^2} + {\left( {y - 0} \right)^2} = {6^2}$
Here $\left( {0,0} \right)$ is the coordinate of the centre and $6$ is the radius of the circle.
Hence, the circle can be drawn in the following manner:
Now, plotting the points on the curve and joining it we get a circle as shown in the figure above.

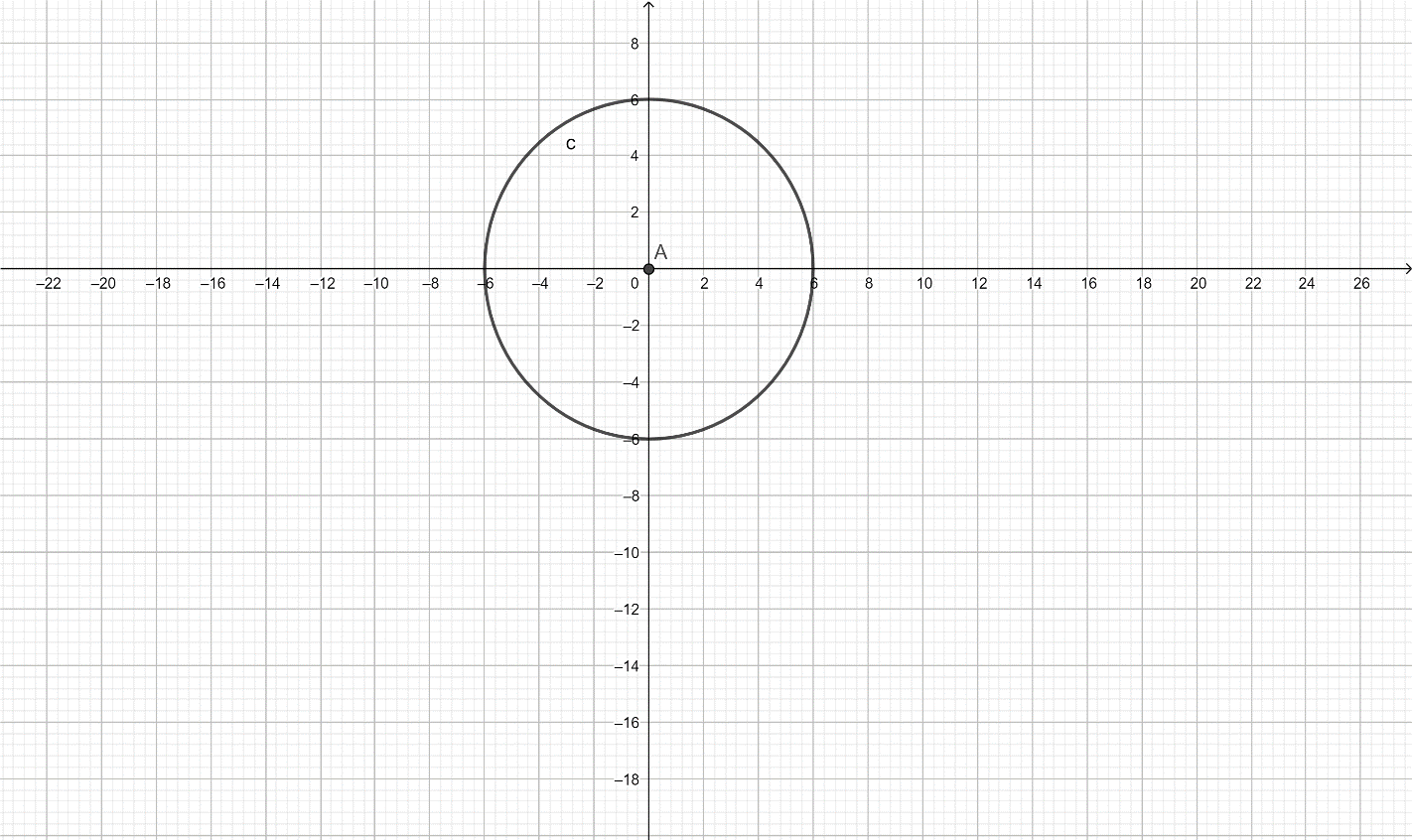
Here the centre lies on the coordinate $\left( {0,0} \right)$ and the radius is of $6$ units.

Note:
The given equation ${x^2} + {y^2} = 36$ represents the locus of a point that moves in such a way that its distance from the point $\left( {0,0} \right)$ is always equal to$6$.
The question can also be solved in a way by putting the values of $x$ and $y$ equal to $0$ simultaneously.
Putting $x\, = \,0$, we will get ${y^2} = 36$ which implies that the value of $y$ is equal to $+ 6\,or\, - 6$
Hence, the coordinates come out to be $\left( {0,6} \right)$ and $\left( {0, - 6} \right)$
Similarly Putting $y\, = \,0$ we will get ${x^2} = 36$ which implies that the value of $x$ is equal to $+ 6\,or\, - 6$.
Hence, the coordinates come out to be $\left( {6,0} \right)$ and $\left( { - 6,0} \right)$
General form of the circle is ${x^2} + {y^2} + 2gx + 2fy + c = 0$ , where $( - g, - f)$ is the centre and $\sqrt {{g^2} + {h^2} - c}$ is the radius of the circle .