Question

How do you graph ${x^2} + {y^2} = 16$ ?

Answer 1

Hint : In order to graph the equation above, subtract the value of variables $x$ and $y$ by zero, and compare the equation obtained from the standard form of the circle, get the point of centre and radius of the circle, and then graph the values in the cartesian plane.

Complete step-by-step answer :
We are given an equation ${x^2} + {y^2} = 16$ .
Since, we know that when zero is subtracted from any number it returns the same number. For example: if zero is subtracted from $a$ , it gives $a - 0 = a$ , which is the same number.
So, for the equation we have above, we can write $x$ and $y$ as $\left( {x - 0} \right)$ and $\left( {y - 0} \right)$ .
Substituting these in the above equation, we get:
${\left( {x - 0} \right)^2} + {\left( {y - 0} \right)^2} = 16$
We know that ${4^2} = 16$ , so replacing $16$ with ${4^2}$ , we get:
${\left( {x - 0} \right)^2} + {\left( {y - 0} \right)^2} = 16 \\\ \Rightarrow {\left( {x - 0} \right)^2} + {\left( {y - 0} \right)^2} = {\left( 4 \right)^2} \;$
Which represents the equation of a circle, as we know that the standard form of a circle is ${\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {\left( r \right)^2}$ , where $\left( {h,k} \right)$ represents the points of the centre on the cartesian plane, and $r$ represents the radius of the circle.
So, comparing the standard equation of circle ${\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {\left( r \right)^2}$ with ${\left( {x - 0} \right)^2} + {\left( {y - 0} \right)^2} = {\left( 4 \right)^2}$ , we get:
$r = 4$
$h = 0$
$k = 0$
$\left( {h,k} \right) = \left( {0,0} \right)$
Drawing a graph for a circle with a centre $\left( {0,0} \right)$ and a radius of $4$ units, and the graph is:

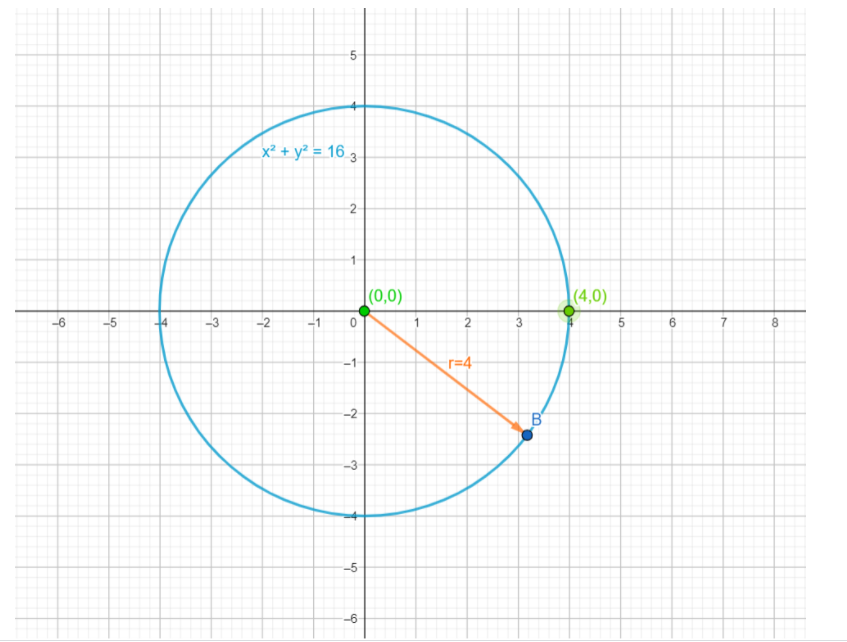
And, the above graph represents the graph of a circle ${x^2} + {y^2} = 16$ with the centre at the origin $\left( {0,0} \right)$ and $radius\left( r \right) = 4$ unit.

Note : Since, the equation given above was the standard form of a circle as the centre was the origin, but if the equation was like ${\left( {x - 3} \right)^2} + {\left( {y + 1} \right)^2} = 25$ , then we will compare it with the standard form of circle to get the point of centre, which would be $\left( {h,k} \right) = \left( {3, - 1} \right)$ and the radius would be $5$ . Then graph the equation with the centre at $\left( {3, - 1} \right)$ taking the radius of $5$ unit.