Question

How do you graph ${x^2} + {y^2} = 16$ ?

Answer 1

Hint : To solve this we need to give the values of ‘x’ and we can find the values of ‘y’. Otherwise we can find the coordinate of the given equation lying on the line of x- axis, we can find this by substituting the value of ‘y’ is equal to zero (x-intercept). Similarly we can find the coordinate of the equation lying on the line of y- axis, we can find this by substituting the value of ‘x’ equal to zero (y-intercept).

Complete step by step solution:
Given, ${x^2} + {y^2} = 16$ .
To find the x-intercept. That is the value of ‘x’ at $y = 0$ . Substituting this in the given equation. We have,
${x^2} + {0^2} = 16$
${x^2} = 16$
Taking square root on both sides we have,
$x = \pm \sqrt {16}$
$x = \pm 4$
Thus we have a coordinate of the equation which lies on the line of x-axis. The coordinate points are $(4,0)$ and $( - 4,0)$ .
To find the y-intercept. That is the value of ‘y’ at $x = 0$ . Substituting this in the given equation we have,
${0^2} + {y^2} = 16$
${y^2} = 16$
Taking square root on both sides we have,
$y = \pm \sqrt {16}$
$y = \pm 4$
Thus we have a coordinate of the equation which lies on the line of the y-axis. The coordinate points are $(0,4)$ and $(0, - 4)$ .
We can see that the given equation ${x^2} + {y^2} = 16$ is a circle equation centre at origin and radius 4.
We have $(4,0)$ , $( - 4,0)$ , $(0,4)$ and $(0, - 4)$ . We point these coordinates and join them with a curve we will obtain a circle.
Let’s plot a graph for this coordinates,

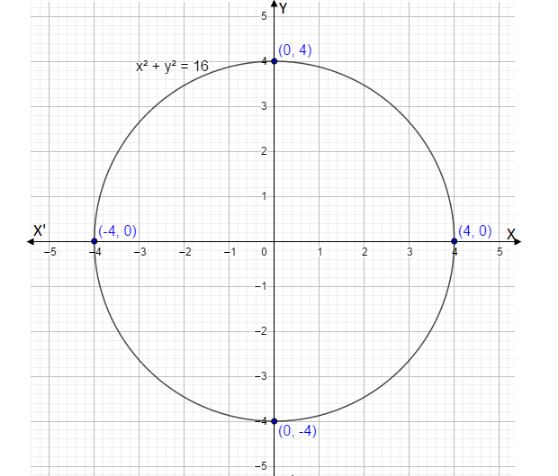
Note : A graph shows the relation between two variable quantities, it contains two axes perpendicular to each other namely the x-axis and the y-axis. Each variable is measured along one of the axes. In the question, we are given one linear equation containing two variables namely x and y, x is measured along the x-axis and y is measured along the y-axis while tracing the given equations.