Solveeit Logo
Login

Question

Question: How do you graph \( {x^2} + {y^2} = 100? \)...

How do you graph x2+y2=100?{x^2} + {y^2} = 100?

Explanation

Solution

To graph the given equation of a circle, use the center radius form of the circle to determine the coordinates of the center and radius of the circle. And to draw a circle, one only needs the coordinates of its center and its radius.
General form of center radius form of a circle is given as
(x−a)2+(y−b)2=r2,  where  (a,  b)  and  r{(x - a)^2} + {(y - b)^2} = {r^2},\;{\text{where}}\;(a,\;b)\;{\text{and}}\;r are the coordinate of the center of the circle and radius of the circle respectively.

Complete step by step solution:
In order to graph the given equation x2+y2=100{x^2} + {y^2} = 100 , we can see that it is an equation of a circle, so in order to graph this equation of a circle we need its coordinates of the center and the radius of the circle. And to find these two, we will compare given equation with the general form of center radius form a circle which is given as
(x−a)2+(y−b)2=r2,  where  (a,  b)  and  r{(x - a)^2} + {(y - b)^2} = {r^2},\;{\text{where}}\;(a,\;b)\;{\text{and}}\;r are the coordinate of the center of the circle and radius of the circle respectively.
Now, coming to the given equation we can express it as
x2+y2=100⇔(x−0)2+(y−0)2=102{x^2} + {y^2} = 100 \Leftrightarrow {(x - 0)^2} + {(y - 0)^2} = {10^2}
On comparing it with general equation, we get the center and radius as
(a,  b)≡(0,  0)  and  r=10(a,\;b) \equiv (0,\;0)\;{\text{and}}\;r = 10
So now, graphing the equation of the circle with help of its center and radius as follows

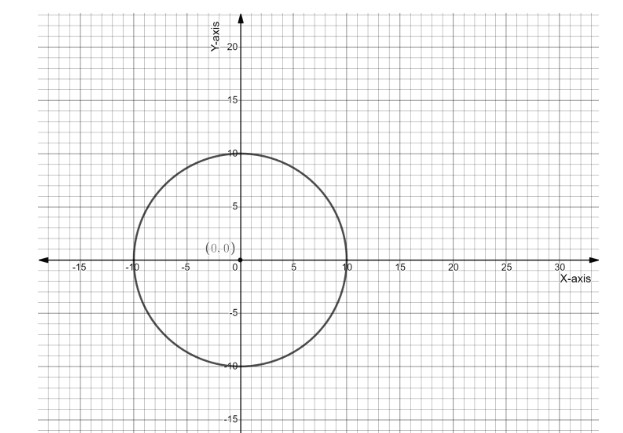
Therefore this is the required graph of the given equation.

Note : Equations having degrees of both independent and dependent variable equal to two, represents a circle. And in order to graph the circle, you should first check if the coefficients of the variables are one or not, if not one then make the coefficients one with help of algebraic operation and then proceed.