Question

How do you graph ${x^2} + {y^2} = 1$

Answer 1

First, substitute some values in $x$ and find the value of $y$. Then taking those values plot the points and join those points. As the given equation represents a circle the graph will be a circle.

Complete step by step solution:
The objective of the problem is to draw the graph of the ${x^2} + {y^2} = 1$
Given equation is ${x^2} + {y^2} = 1$
The above equation represents a circle with centre at origin and with radius one.
About circle: The circle is a combination of points that lie equidistant from one point that is center.
There are three parts in a circle. Those are secant, chord and diameter. A secant is a line that touches the circle at two points. A line segment whose endpoints are on the circle is called a chord. A chord that passes through the centre of the circle is called diameter. The centre of the circle is also called as the focus of the circle. A tangent is a line segment where it touches at only one point.
The general form of the circle is ${\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}$ . where $h,k$ are the centre of the circle and $r$ is the radius of the circle.
Now converting the given equation ${x^2} + {y^2} = 1$ into the general form of the circle.
${\left( {x - 0} \right)^2} + {\left( {y - 0} \right)^2} = {1^2}$
On comparing with general form of the circle we get
The centre is (0,0) and the radius of the circle is 1.
Now plotting the graph of the given circle.

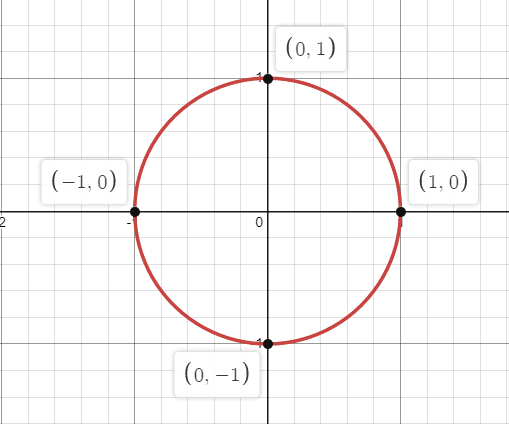
The graph represents the circle with radius one and centered at (1,1).

Note: The radius around the circle is called circumference of the circle. A complete circle is 360 degrees. The area of the circle is $\pi {r^2}$. The circumference of the circle is $\pi d$ where d is the diameter. the perimeter of the circle is $2\pi r$ .