Solveeit Logo
Login

Question

Question: How do you graph \[{{x}^{2}}+{{\left( y-1 \right)}^{2}}=1\] ?...

How do you graph x2+(y−1)2=1{{x}^{2}}+{{\left( y-1 \right)}^{2}}=1 ?

Explanation

Solution

As we can see that this question is from the topic of geometry. And the equation in the given question is the form of the equation of circle. Before solving this question, first let us know the general equation of the circle. The general equation of circle is (x−x1)2+(y−y1)2=r2{{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}={{r}^{2}} , where (x1,y1)\left( {{x}_{1}},{{y}_{1}} \right) is the centre of the circle and rr is the radius of the circle.

Complete step-by-step solution:
Let us solve this question. In this question, we have to draw the graph of the equation x2+(y−1)2=1{{x}^{2}}+{{\left( y-1 \right)}^{2}}=1. As we can see, this equation looks like the equation of a circle.
The general equation of the circle is (x−x1)2+(y−y1)2=r2{{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}={{r}^{2}}, where (x1,y1)\left( {{x}_{1}},{{y}_{1}} \right) is the centre point of that circle and rr is the length of radius of the same circle.
Now, let us know that what will be the graph of this general equation of circle (x−x1)2+(y−y1)2=r2{{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}={{r}^{2}}.

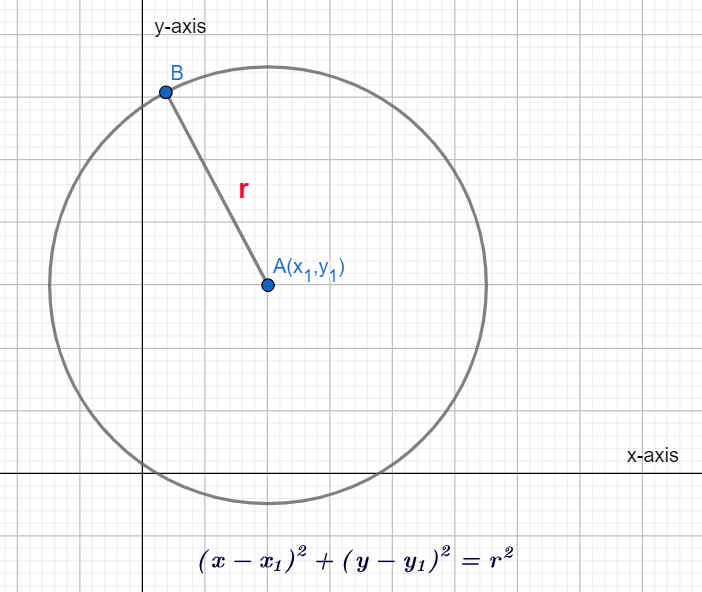
As we can see from the above graph that the circle of equation (x−x1)2+(y−y1)2=r2{{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}={{r}^{2}} is having the centre as (x1,y1)\left( {{x}_{1}},{{y}_{1}} \right) and r as radius of circle.
Now, we will find the graph for the equation of circle x2+(y−1)2=1{{x}^{2}}+{{\left( y-1 \right)}^{2}}=1. This equation also can be written as (x−0)2+(y−1)2=12{{\left( x-0 \right)}^{2}}+{{\left( y-1 \right)}^{2}}={{1}^{2}} .
Here, we can see from the above equation that the centre of the circle will be (0,1)\left( 0,1 \right) and the length of the radius will be 1.
Now, we find the graph for the equation x2+(y−1)2=1{{x}^{2}}+{{\left( y-1 \right)}^{2}}=1
So, the graph of the equation x2+(y−1)2=1{{x}^{2}}+{{\left( y-1 \right)}^{2}}=1 will be:

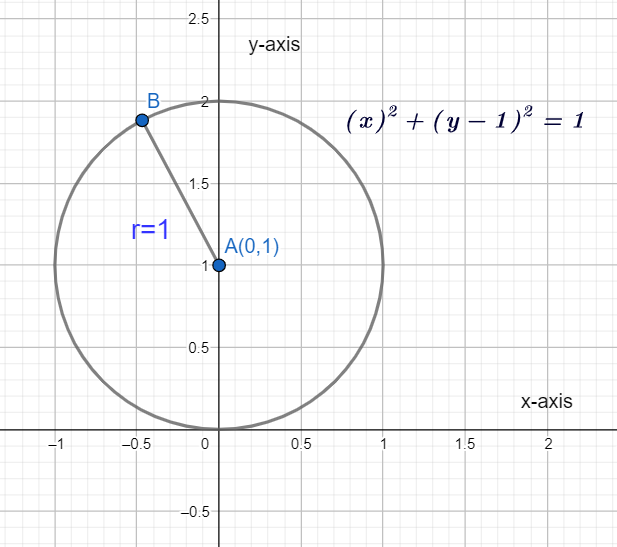
Hence, we get the graph of the equation.

Note: One should have a better knowledge in the topic of circle chapter to solve these types of questions easily. General equation of a circle should be kept remembered. The general equation of circle is (x−x1)2+(y−y1)2=r2{{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}={{r}^{2}}, where (x1,y1)\left( {{x}_{1}},{{y}_{1}} \right) is the centre and r is the radius of the circle.