Question

How do you graph $x = - 10$ using intercepts?

Answer 1

Here, we need to graph the given line. We will take the abscissa and ordinate 0 to find the intercepts, and use them to draw the graph of the given equation. The abscissa of a point $\left( {x,y} \right)$ is $x$, and the ordinate of a point $\left( {x,y} \right)$ is $y$.

Complete step-by-step solution:
First, we will find the intercepts of the given line.
Rewriting the equation, we get
$x + 0 \times y = - 10$
Substituting 0 for $y$ in the equation, we get
$x + 0 \times 0 = - 10$
Therefore, we get
$x = - 10$
The $x$-intercept of the given line is $- 10$.
This means that the line touches the $x$-axis at the point $\left( { - 10,0} \right)$.
Substituting 0 for $x$ in the equation, we get
$0 + 0 \times y = - 10$
Therefore, we get
$0 = - 10$
This is incorrect.
The given line has no $y$-intercept.
Therefore, there is no point on the given line that has the abscissa 0.
This means that the line does not touch the $y$-axis at any point.
When two straight lines do not touch each other at any point, they are called parallel lines.
This means that the graph of the line $x = - 10$ is parallel to the $y$-axis.
Now, we will draw the graph of the given line.
The graph of the line $x = - 10$ touches the $x$-axis at the point $\left( { - 10,0} \right)$, and is parallel to the $y$-axis.
The value of $x$ remains $- 10$ for all values of $y$.
Drawing the graph of the line $x = - 10$, we get

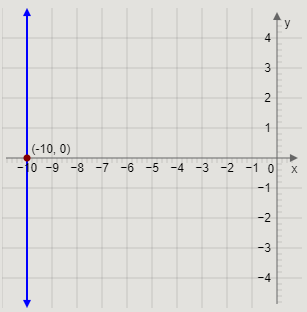
This is the required graph of the line $x = - 10$.

Note:
We can also rewrite the equation using the intercept form of a line.
The intercept form of a line is given by $\dfrac{x}{a} + \dfrac{y}{b} = 1$, where $a$ and $b$ are the $x$-intercept and $y$-intercept cut by the straight line respectively.
Dividing both sides of the given equation by $- 10$, we get
$\dfrac{x}{{ - 10}} = 1$
Here, $- 10$ is the $x$-intercept, and there is no $y$-intercept.