Question

How do you graph $x<-0.5$?

Answer 1

We try to take points which have x coordinates less than $-0.5$. There is no restriction on the y coordinates. Based on the points we try to find the space or region in the 2-D plane which satisfies $x<\- 0.5$.

Complete step by step solution:
The inequation $x<-0.5$ represents the space or region in 2-D plane where the x coordinates of points are valued less than $-0.5$.
We first take some points for the x coordinates where $x<-0.5$.
The values will be $x=-1,-2,-5,-10$.
We can take the y coordinate anything we want. The inequation is only based on the values of the x coordinates.
So, for y coordinate we take $y=-2,5,0,-10$ respectively for the x coordinates $x=-1,-2,-5,-10$
The points are $\left( x,y \right)=\left( -1,-2 \right);\left( -2,5 \right);\left( -5,0 \right);\left( -10,-10 \right)$.
We put these points in the graph to get
Based on the points we can measure the region.
Now we try to draw the line $x=-0.5=-\dfrac{1}{2}$.
Then we take all the x coordinates which have less value than $x=-\dfrac{1}{2}$.

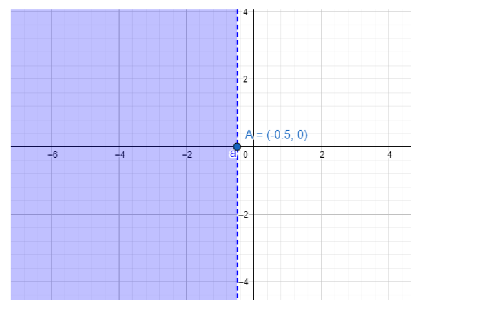
The dotted line is the equation $x=-\dfrac{1}{2}$. All the points on the left side have x coordinates valued less than $x=-\dfrac{1}{2}$.
So, all those points on the marked area are solutions to the inequation $x <-0.5$.

Note: We can also express the inequality as the interval system where $x<-0.5$ defines that $x\ in \left( -\infty ,-0.5 \right)$. The interval for the y coordinates will be anything which can be defined as $y\in \left( -\infty ,\infty \right)$. We also need to remember that the points on the line $x=-0.5$ will not be the solution for the inequation.