Question

How do you graph using the slope and intercept of $6x+5y=2$ ?

Answer 1

Hint : We have given an equation of a line as $6x+5y=2$ , which is a straight-line equation. In order to draw a graph of the given equation, first rewrite the given equation in the slope intercept form and later identify the slope and the y-intercept and the x-intercept. A straight-line equation is always linear and represented as $y=mx+c$ where $m$ is the slope of the line and $c$ is the y-intercept and $\dfrac{-c}{m}$ is the x-intercept.
Now, getting the points we can easily plot the graph of the given straight line equation.

Complete step-by-step answer :
We have equation of line,
$6x+5y=2$
Rewrite the above equation in a slope intercept form, i.e. $y=mx+c$
$y=-\dfrac{6}{5}x+\dfrac{2}{5}$
Now we compare this given equation with the general linear equation i.e., $y=mx+c$
Hence,
Slope of the given line, $m=-\dfrac{6}{5}$ .
y-intercept of the given line , $c=\dfrac{2}{5}$ .
Therefore, we can say that point $(0,\dfrac{2}{5})$ lie on the line.
x-intercept of the given line ,
$\dfrac{-c}{m}=\dfrac{-\dfrac{2}{5}}{-\dfrac{6}{5}}=-\dfrac{2}{5}\times -\dfrac{5}{6}=\dfrac{1}{3}$ .
Therefore, we can say that point $(\dfrac{1}{3},0)$ lie on the line.
With the help of two points, we can plot the graph by connecting the points as follow,

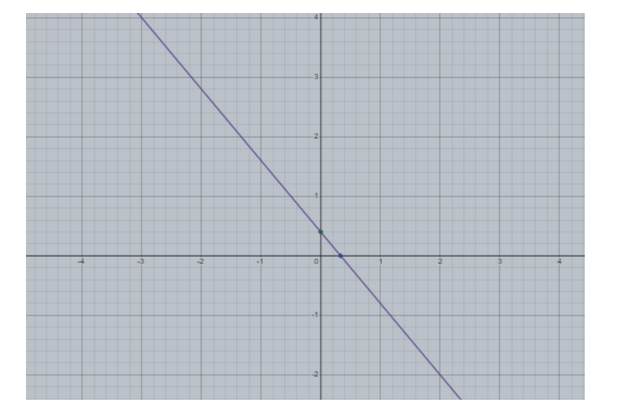
Note : Slope intercept form is a form of writing an equation of a straight line. This type of linear equation is sometimes called a slope-intercept form because we can easily find the slope and the intercept of the corresponding lines. This also allows us to graph it. While we write any equation in this form, we usually get the values of slope and the intercept of the given straight line. We can quickly tell the slope i.e., $m$ the y-intercepts i.e., $(y,0)$ and the x-intercept i.e., $(0,y)$ .we can graph the corresponding line .
Slope of a line can also be found if two points on the line are given. Let the two points on the line be $({{x}_{1}},{{y}_{1}}),({{x}_{2}},{{y}_{2}})$ respectively.
Then slope is given by, $m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ .
Slope is also defined as the ratio of change in $y$ over the change in $x$ between any two points.
y-intercept can also be found by substituting $x=0$ .
Similarly, x-intercept can also be found by substituting $y=0$ .