Question

How do you graph using the slope and intercept of $-8x+2y=4$ ?

Answer 1

Hint : we have given an equation of a line as $-8x+2y=4$ , which is a straight-line equation. In order to draw a graph of the given equation, we will need to write the equation in a slope intercept form. A straight-line equation is always linear and represented as $y=mx+c$ where $m$ is the slope of the line and $c$ is the y-intercept and $\dfrac{-c}{m}$ is the x-intercept.
Now, getting the points we can easily plot the graph of the given straight line equation.

Complete step-by-step answer :
We have equation of line,
$-8x+2y=4$
Rewrite the above equation in a slope intercept form, i.e. $y=mx+c$
$y=4x+2$
Now we compare this given equation with the general linear equation i.e., $y=mx+c$
Hence ,
Slope of the given line, $m=4$ .
y-intercept of the given line , $c=2$ .
Therefore, we can say that point $(0,2)$ lies on the line.
x-intercept of the given line , $\dfrac{-c}{m}=\dfrac{-2}{4}=-\dfrac{1}{2}$ .
Therefore, we can say that point $(\dfrac{-1}{2},0)$ lies on the line.
With the help of two points, we can plot the graph by connecting the points as follow,

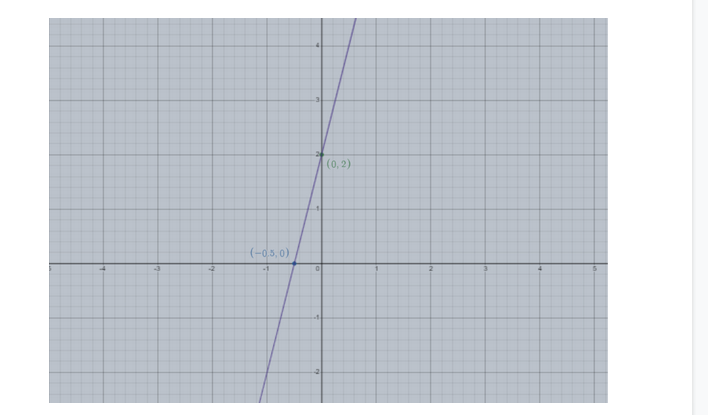
Note : Slope of a line can also be found if two points on the line are given. Let the two points on the line be $({{x}_{1}},{{y}_{1}}),({{x}_{2}},{{y}_{2}})$ respectively.
Then slope is given by, $m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ .
Slope is also defined as the ratio of change in $y$ over the change in $x$ between any two points.
y-intercept can also be found by substituting $x=0$ .
Similarly, x-intercept can also be found by substituting $y=0$ .