Question

How do you graph using slope and intercept of $x+2y=6$ ?

Answer 1

To graph $x+2y=6$ using its slope and intercept, we will to represent the given equation in slope-intercept form. Slope-intercept form is given as $y=mx+c$ , where m is the slope and c is the y-intercept. Taking its y-intercept value gives a point. To get the next point, we have to find the x-intercept by substituting $y=0$ in the obtained slope-intercept form.

Complete step by step solution:
We have to graph $x+2y=6$ using its slope and intercept. Firstly, we have to represent the given equation in slope-intercept form. We know that slope-intercept form is given as $y=mx+c$ , where m is the slope and c is the y-intercept. Hence, we can write the given equation as
$\Rightarrow 2y=6-x$
Let us take 2 from LHS to RHS.
$\begin{aligned} & \Rightarrow y=\dfrac{6-x}{2} \\\ & \Rightarrow y=\dfrac{-1}{2}x+3...\left( i \right) \\\ \end{aligned}$
When we compare the above equation to the slope-intercept form, we can see that $m=-\dfrac{1}{2}$ and y-intercept, $c=3$ . Hence, one point will be $\left( 0,3 \right)$ .
Now, we have to find the x-intercept. For this, we will substitute $y=0$ in equation (i).
$\Rightarrow 0=\dfrac{-1}{2}x+3$
Let us take 3 from RHS to LHS. We will get
$\Rightarrow -3=\dfrac{-1}{2}x$
Now, we can cancel the negative sign from both sides.
$\Rightarrow 3=\dfrac{1}{2}x$
Let us take $\dfrac{1}{2}$ from RHS to LHS.
$\Rightarrow x=6$
Hence, the other point is $\left( 6,0 \right)$ .
Let us graph this.

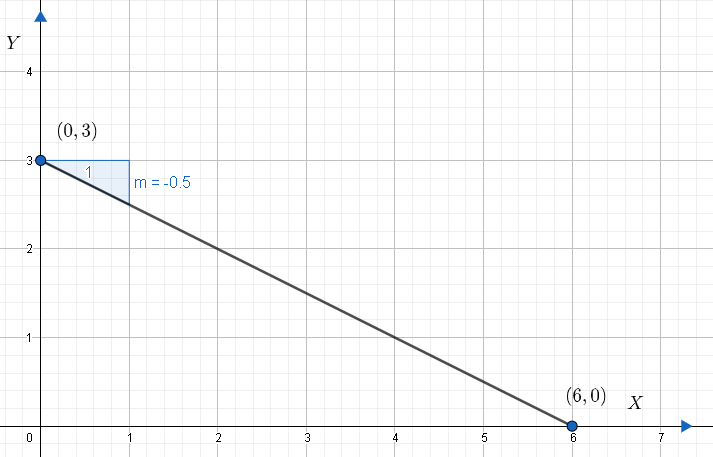
Note: Students must be thorough with the slope-intercept form. ‘c’ in the slope-intercept form in the y-intercept not x-intercept. We can see from the graph that the slope is $-\dfrac{1}{2}$ . We can find the slope from the graph by considering 2 points and using the equation $m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ .