Question

How do you graph using slope and intercept of $8x - 6y = - 20$ ?

Answer 1

Hint : Here in this given equation is a linear equation. Here we have to plot a graph using slope and intercept, to this first solve for one variable. To solve this equation for y by using arithmetic operation we can shift the x variable to RHS then the resultant equation will be in the form of $y = mx + b$ later we can plot the graph for the resultant equation.

Complete step by step solution:
The given equation is a linear equation. These equations are defined for lines in the coordinate system. An equation for a straight line is called a linear equation. The general representation of the straight-line equation is $y = mx + b$ , it involves only a constant term and a first-order (linear) term, where m is the slope and b is the y-intercept. Occasionally, this equation is called a "linear equation of two variables," where y and x are the variables.
Consider the given equation
$\Rightarrow 8x - 6y = - 20$
Rearrange the equation because we have to shift the variable x and its coefficient to the RHS so subtract 8x on both side, then
$\Rightarrow 8x - 6y - 8x = - 20 - 8x$
On simplification, we get
$\Rightarrow - 6y = - \left( {8x + 20} \right)$
Cancel $' - '$ ve sign on both side, then
$\Rightarrow 6y = 8x + 20$
Divide both side by 6
$\Rightarrow \dfrac{6}{6}y = \dfrac{8}{6}x + \dfrac{{20}}{6}$
On simplification, we get
$\Rightarrow y = \dfrac{4}{3}x + \dfrac{{10}}{3}$
Comparing the above equation with the straight-line equation is $y = mx + b$ .
Slope: $m = \dfrac{4}{3}$ and
y- intercept: $\left( {0,\dfrac{{10}}{3}} \right)$
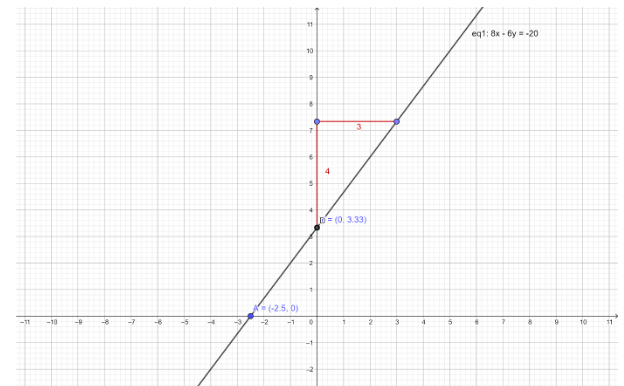
the graph of the equation $y = \dfrac{4}{3}x + \dfrac{{10}}{3}$ using slope and intercept is given by:
when $x = 0$ then $y = \dfrac{{10}}{3}$
therefore, $\left( {x,y} \right) = \left( {0,\dfrac{{10}}{3}} \right) = \left( {0,3.33} \right)$
when, $y = 0$ then $x = - \dfrac{{10}}{3} \times \dfrac{3}{4} \Rightarrow x = - \dfrac{5}{2}$
therefore, $\left( {x,y} \right) = \left( { - \dfrac{5}{2},0} \right) = \left( { - 2.5,0} \right)$

Note : The algebraic equation or an expression is a combination of variables and constants, it also contains the coefficient. The alphabets are known as variables. The x, y, z etc., are called as variables. The numerals are known as constants. The numeral of a variable is known as co-efficient. We have 3 types of algebraic expressions namely monomial expression, binomial expression and polynomial expression. By using the tables of multiplication, we can solve the equation.