Question

How do you graph using slope and intercept of $- 5x + y = 0$?

Answer 1

In this question we have to graph of the line using the slope and intercepts of the line given, we can do this by first finding the slope and intercept of the line by using Slope-intercept form which is given by $y = mx + b$ , where $m$ is the slope of the line and $b$ is the y-intercept of the line, now plot the point and slope on the graph we will get the required graph.

Complete step by step solution:
Given equation of the line is $- 5x + y = 0$,
Now convert the equation given into slope intercept form which is given by $y = mx + b$ , where $m$ is the slope of the line and $b$ is the y-intercept of the line,
So, given equation is $- 5x + y = 0$,
Now add $5x$ from both sides of the equation we get,
$\Rightarrow - 5x + y + 5x = 0 + 5x$,
Now simplifying we get,
$\Rightarrow y = 5x$,
Now rewriting the equation we get,
$\Rightarrow y = 5x + 0$, this is in form of slope intercept form,
Now comparing the equation with the slope intercept form which is $y = mx + b$,
On comparing here $m = 5$ and $b = 0$,
So we know that m is the slope of the line, now here $5$is the slope of the given line, and the intercept of the line is $\left( {0,0} \right)$,
Now plotting the points on the graph we get,

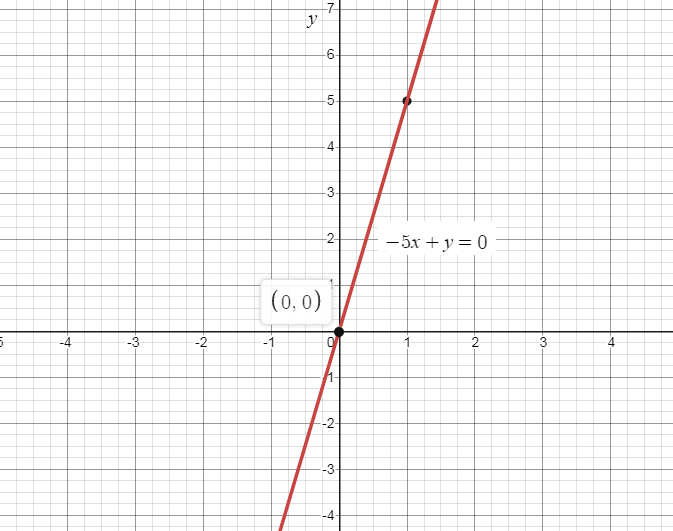
Note: Remember that if the slope of a line is equal to zero then it is parallel to x-axis and if the slope tends to infinity then it is perpendicular to x-axis. Also, we can remember that if the x-coordinates of the two points through which the line passes are same it must be perpendicular to the x-axis and if y-coordinates of the two points through which the line passes are same it must be parallel to the x-axis.