Question

How do you graph $\theta =\dfrac{\pi }{3}$ ?

Answer 1

The graph of $\theta =\dfrac{\pi }{3}$ is in polar form graph, where $\theta$ is the angle between line segment joining point and origin with positive X axis. The graph of $\theta =\dfrac{\pi }{3}$ is the collection of all points which makes an angle of $\dfrac{\pi }{3}$ with positive X axis when joined with origin. So we can be sure that all the points are in the first quadrant.

Complete step by step answer:
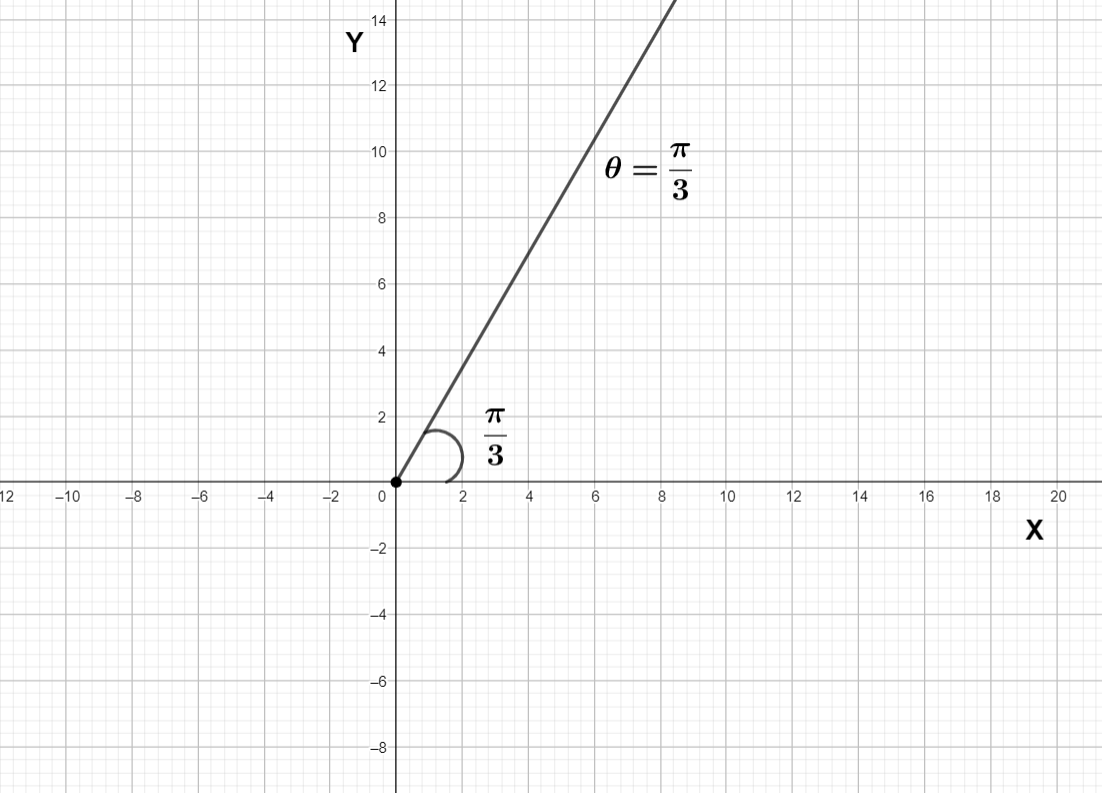
We have drawn the graph of $\theta =\dfrac{\pi }{3}$ , it is the locus of all points which makes angle of $\dfrac{\pi }{3}$ with positive X axis when it is joined with origin , so all such points lie in the first quadrant.
Let’s the point is (x, y) is lie on the graph $\theta =\dfrac{\pi }{3}$ where x, y are positive
So the line joining (x, y) and origin makes an angle $\dfrac{\pi }{3}$ with positive X axis
So we can write ${{\tan }^{-1}}\dfrac{y}{x}=\dfrac{\pi }{3}$
So $\tan \dfrac{\pi }{3}=\dfrac{y}{x}$ where x and y are positive
$\dfrac{y}{x}=\sqrt{3}$
$\Rightarrow y=\sqrt{3}x$
So the graph of $\theta =\dfrac{\pi }{3}$ is equal to the graph of $y=\sqrt{3}x$ in first quadrant
Now let’s draw the graph of $y=\sqrt{3}x$ in first quadrant

Note: While converting a polar coordinate form equation into a simple equation, always focus on the quadrant, in which quadrant the graph should be done. In polar form $\tan \theta$ is equal to $\dfrac{y}{x}$ and the value of r is equal to $\dfrac{y}{x}$ . The given equation that we have drawn a graph for is independent of r where $\theta$ is constant. The value of $\theta$ can give us the quadrant. If the value of $\theta$ is between 0 to $\dfrac{\pi }{2}$ it is in first quadrant, next interval of $\dfrac{\pi }{2}$ is second quadrant and this goes on to fourth quadrant.