Question

How do you graph $\theta = - \dfrac{{5\pi }}{6}$?

Answer 1

We are given the measure of an angle. We have to plot the graph of the expression. First, find the relation between the polar and Cartesian coordinates. Then, divide the y coordinate by the x coordinate. Then, substitute the value of $\theta$ to determine the y coordinates in terms of x. Then, plot the graph of obtained coordinate.

Complete step by step solution:
Given the measure of an angle, $\theta = - \dfrac{{5\pi }}{6}$.

Determine the relation between the polar and Cartesian coordinates

$\Rightarrow x = r\cos \theta$ …… (1)

$\Rightarrow y = r\sin \theta$ …… (2)

Now, divide the equation (2) by equation (1), we get:

$\Rightarrow \dfrac{y}{x} = \dfrac{{r\sin \theta }}{{r\cos \theta }}$

On simplifying the expression, we get:

$\Rightarrow \dfrac{y}{x} = \tan \theta$

Now, we will substitute $\theta = - \dfrac{{5\pi }}{6}$ into the expression.

$\Rightarrow \dfrac{y}{x} = \tan \left( { - \dfrac{{5\pi }}{6}} \right)$

Now, apply the property $\tan \left( { - \theta } \right) = - \tan \left( \theta \right)$.

$\Rightarrow \dfrac{y}{x} = - \tan \left( {\dfrac{{5\pi }}{6}} \right)$

Now, we will substitute $\dfrac{1}{{\sqrt 3 }}$ for $\tan \left( {\dfrac{{5\pi }}{6}} \right)$ into the expression.

$\Rightarrow \dfrac{y}{x} = - \dfrac{1}{{\sqrt 3 }}$

Rationalize the denominator to remove the radical expression at the denominator.

$\Rightarrow \dfrac{y}{x} = - \dfrac{1}{{\sqrt 3 }} \times \dfrac{{\sqrt 3 }}{{\sqrt 3 }}$

On simplifying the expression, we get:

$\Rightarrow \dfrac{y}{x} = - \dfrac{{\sqrt 3 }}{3}$

Now, solve the equation for y.

$\Rightarrow y = - \dfrac{{\sqrt 3 }}{3}x$

Now, we will plot the graph of the equation.

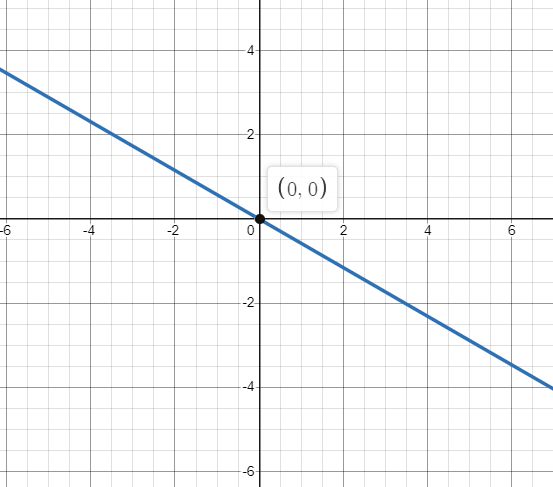
It is observed that the graph of $\theta = - \dfrac{{5\pi }}{6}$ is a straight line passing through the origin.

Note: The students please note that the polar equation gives the relation between r and $\theta$ where r is the distance from the origin to a particular point on the curve. The value of $\theta$ represents the counterclockwise angle made by a point on the curve and the positive x-axis. The students must also remember that when the angle is given with minus sign then we have to apply the properties of trigonometric functions:
$\begin{gathered} \sin \left( { - \theta } \right) = - \sin \theta \\\ \cos \left( { - \theta } \right) = \cos \theta \\\ \tan \left( { - \theta } \right) = - \tan \theta \\\ \csc \left( { - \theta } \right) = - \csc \theta \\\ \sec \left( { - \theta } \right) = \sec \theta \\\ \cot \left( { - \theta } \right) = - \cot \theta \\\ \end{gathered}$
Please note that to convert a polar coordinate $\left( {r,\theta } \right)$ into Cartesian form $\left( {x,y} \right)$ we can use the formula:
$\Rightarrow x = r\cos \theta$ and $y = r\sin \theta$