Question

How do you graph the $y = - \sec \left( {2x} \right)$ ?

Answer 1

A graph of a function f is the set of ordered pairs; the equation of graph is generally represented as $y = f\left( x \right)$ , where x and $f\left( x \right)$ are real numbers. We substitute the value of x and we determine the value of y and then we mark the points in the graph and we join the points.

Complete step by step solution:
Here, in the given question, we have to plot the graph for the given function. A graph of a function is set of ordered pairs and it is represented as $y = f\left( x \right)$, where x and $f\left( x \right)$ are real numbers. These pairs are in the form of Cartesian form and the graph is the two-dimensional graph.
First, we have to find the value of y by using the graph equation $y = - \sec \left( {2x} \right)$.
Let us substitute the value of x as $\dfrac{\pi }{2}$.
$\Rightarrow y = - \sec \left( {2 \times \dfrac{\pi }{2}} \right)$
$\Rightarrow y = - \sec \pi$
$\Rightarrow y = - \left( { - 1} \right)$
$\Rightarrow y = 1$
Now we consider the value of x as $\dfrac{\pi }{3}$, the value of y is
$\Rightarrow y = - \sec \left( {2 \times \dfrac{\pi }{3}} \right)$
$\Rightarrow y = - \sec \left( {\dfrac{{2\pi }}{3}} \right)$
$\Rightarrow y = 2$
Now we consider the value of x as $\left( {\dfrac{\pi }{6}} \right)$, the value of y is
$\Rightarrow y = - \sec \left( {2 \times \dfrac{\pi }{6}} \right)$
$\Rightarrow y = - \sec \left( {\dfrac{\pi }{3}} \right)$
$\Rightarrow y = - 2$
Now we consider the value of x as $0$, the value of y is
$\Rightarrow y = - \sec \left( {2 \times 0} \right)$
$\Rightarrow y = - 1$
Now we draw a table for these values we have

X	$\dfrac{\pi }{2}$	$\dfrac{\pi }{3}$	$\left( {\dfrac{\pi }{6}} \right)$	$0$
y	$1$	$2$	$- 2$	$- 1$

We, also know the nature of the graph of sine function. Hence, we can now plot the graph of the given function $y = - \sec \left( {2x} \right)$. The nature of the graph of a function and its slope can also be determined from the derivative of the function. The graph plotted for these points is represented below:

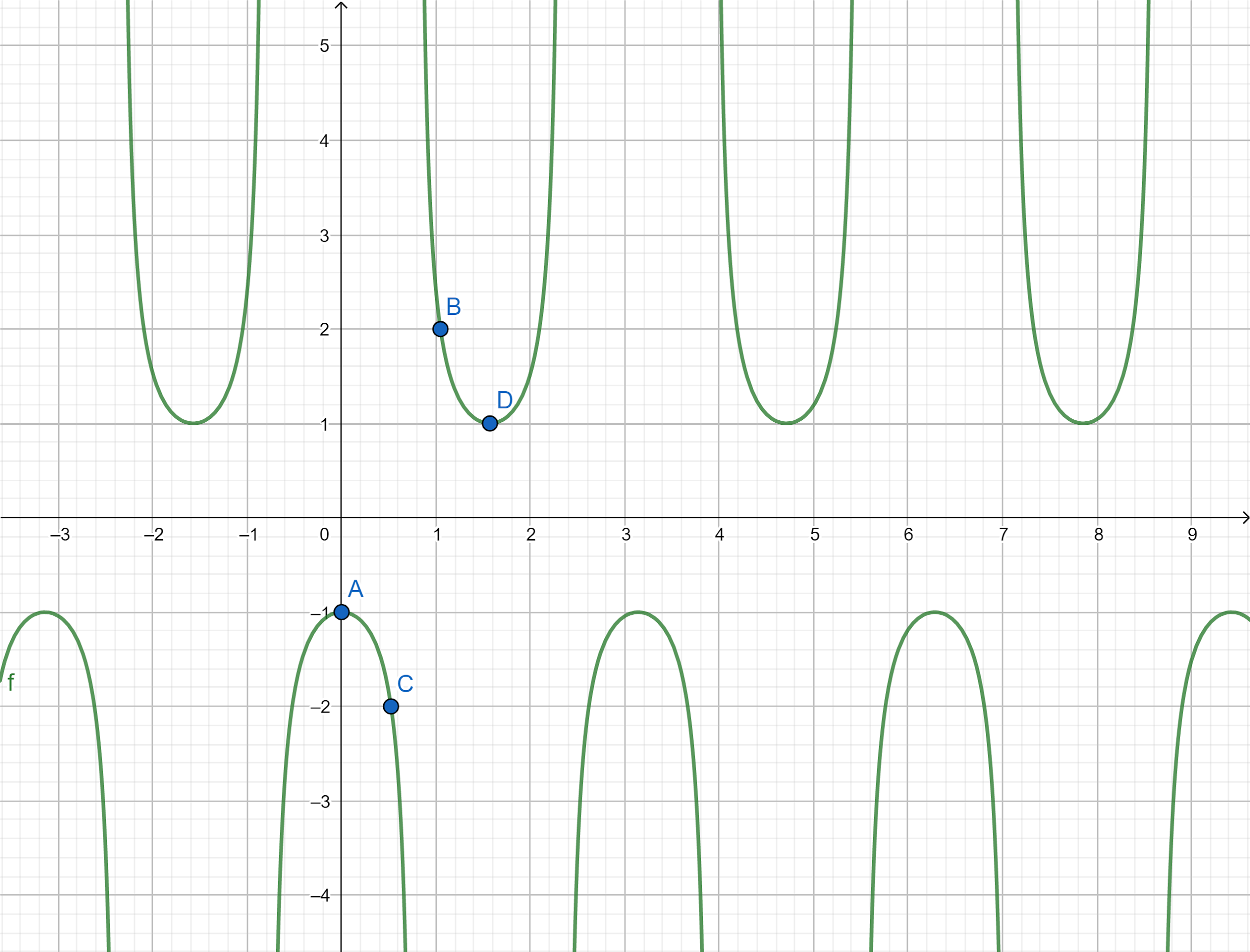
Note: The graph is plotted x-axis versus y axis. The graph is two dimensional. By the equation of a graph, we can plot the graph by assuming the value of x. We can’t assume the value of y. because the value of y depends on the value of x. hence, we have plotted the graph.