Question

How do you graph the point $\left( -4,-4,3 \right)$ ?

Answer 1

To locate a point in a plane, two numbers are necessary. We know that any point in the plane can be represented as an ordered pair $\left( a,b \right)$ of real numbers, where a is the $x$-coordinate and b is the $y$-coordinate. For this reason, a plane is called two-dimensional. To locate a point in space, three numbers are required. We represent any point in space by an ordered triple $\left( a,b,c \right)$ where $a,b,c$ are real numbers. Let us use this to plot the point.

Complete step by step solution:
In order to represent points in space, we first choose a fixed point $O$ called the origin and three directed lines through $O$ that are perpendicular to each other, called the coordinate axes and labeled the $x$-axis, $y$-axis, and $z$-axis.
Usually we think that the $x,y$ axes lie on the plane of a paper which are perpendicular to each other. And the $z$-axis is either coming out of the plane of paper or directed into the plane of paper.
The $xy$-plane is the plane that contains the $x$ and $y$-axes, the $yz$-plane contains the $y$- and $z$-axes, the $xz$ -plane contains the $x$- and $z$-axes.
Now if $P$ is any point in space, let $a$ be the (directed) distance from the $yz$-plane to $P$, let $b$be the distance from the $xz$-plane to $P$, and let $c$be the distance from the $xy$-plane to $P$. We represent the point $P$ by the ordered triple ($a$, $b$, $c$) of real numbers and we call $a$, $b$, and $c$ the coordinates of $P$, $a$ is the $x$-coordinate, $b$is the $y$-coordinate, and $c$ is the $z$-coordinate.
Let us assume that our point to be $P\left( -4,-4,3 \right)$ .
$-4$ is the $x$-coordinate. $-4$ is the $y$-coordinate. $3$ is the $z$-coordinate.
Graph :

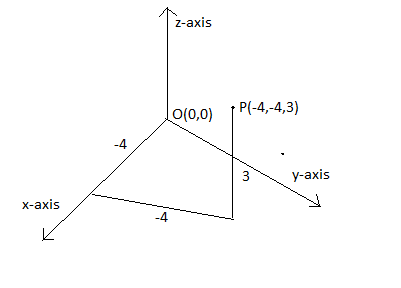
Note: Usually, three coordinates is not asked in the exam since it is three dimensional. And we can’t show three dimensional on a piece of paper as paper is only three dimensional. But being able to imagine $z$-axis could be highly useful to solve problems in physics and would also need the third axis to solve higher level mathematics. Practice is required to plot three kinds of points and to be able to imagine the axis.