Question

How do you graph the parabola $y = {x^2} - 4x + 4$ using vertex, intercepts and additional points?

Answer 1

This problem deals with finding the vertex, $x$ and $y$ intercepts , and the additional points of the given parabola equation. The general equation of the parabola is given by $y = a{x^2} + bx + c$, whereas the vertex form of parabola equation $y = a{\left( {x - h} \right)^2} + k$, where the vertex coordinates are given by $\left( {h,k} \right)$.

Complete step-by-step solution:
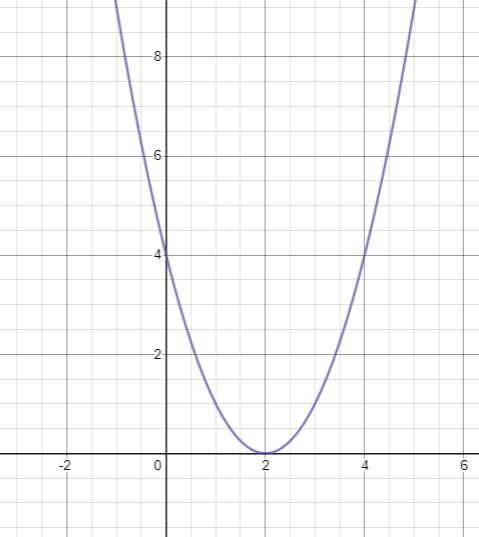
Given the equation of the parabola which is given by $y = {x^2} - 4x + 4$.
The standard or general form of vertex form of equation is given by $y = a{\left( {x - h} \right)^2} + k$, where the vertex of the parabola is $\left( {h,k} \right)$.
First consider the given parabola equation as shown below:
$\Rightarrow y = {x^2} - 4x + 4$
$\Rightarrow y = {\left( {x - 2} \right)^2}$
On comparing the above equation with the standard vertex form of parabola $y = a{\left( {x - h} \right)^2} + k$, the vertex of the parabola $y = {\left( {x - 2} \right)^2}$ is given by:
$\Rightarrow \left( {h,k} \right) = \left( {2,0} \right)$
So the vertex of the parabola $y = {x^2} - 4x + 4$ is equal to $\left( {2,0} \right)$.
Now the y-intercept of the parabola is found by substituting the x-coordinate as zero in the equation of the parabola, as shown below:
$\Rightarrow y = {\left( {x - 2} \right)^2}$
At $x = 0$, $y = 4$, so the y-intercept of the parabola is equal to $\left( {0,4} \right)$.
Similarly the x-intercept of the parabola is found by substituting the y-coordinate as zero in the equation of the parabola, as shown below:
$\Rightarrow y = {\left( {x - 2} \right)^2}$
At $y = 0$, $x = 2$, so the y-intercept of the parabola is equal to $\left( {2,0} \right)$.
The distance of vertex from directrix $d$, is equal to $\dfrac{1}{{4a}}$, here $a$ is equal to 1, from the given equation of the parabola.
$\Rightarrow d = \dfrac{1}{{4a}}$
$\therefore d = \dfrac{1}{4}$
$\because a = 1$
We know that the length of the parabola’s latus rectum is equal to $4d$, from the above expressions the value of $4d = 1$, here $d$ is the distance from the focus to the vertex.
The ends of the latus rectum are $\left( {1.5,0.25} \right)$ and $\left( {2.5,0.25} \right)$.

Note: Please note that the intercepts of the parabola are found by substituting one of the coordinates as zero, to find the intercepts of the other coordinate. For the general equation of the parabola ${y^2} = 4ax$ or ${x^2} = 4ay$ , the vertex is the origin which is the point $\left( {0,0} \right)$.