Question

How do you graph the parabola $y = {x^2} - 4$ using vertex, intercepts and additional points?

Answer 1

This problem is related to conic sections. A curve which is obtained by intersection of the surface of a cone with a plane is known as a conic section. The parabola, the hyperbola and the ellipse are the three types of conic sections. The given problem deals with one of the types of conic section i.e., the parabola. The general standard equation of a parabola is ${x^2} = 4ay$.

Complete step by step solution:
Given parabola, $y = {x^2} - 4$.
First, we need to rewrite the given equation in vertex form i.e., $y = a{\left( {x - h} \right)^2} + k$ and then, determine the values of $a,h$ and $k$.
$y = {\left( {x + 0} \right)^2} - 4$
Here, $a = 1,h = 0$ and $k = - 4$.
Since the value of $a$ is positive, it means that the parabola opens up.
We know the vertex $\left( {h,k} \right)$ is $\left( {0, - 4} \right)$-----(1)
We now find the distance $p$, from the vertex to the focus. The distance from vertex to a focus of a parabola can be calculated using formula: $\dfrac{1}{{4a}}$. Substituting the value of$a$in the formula and we get,
$\dfrac{1}{{4 \times 1}} = \dfrac{1}{4}$
$p = \dfrac{1}{4}$------(2)
Next, we find the focus of the parabola. This can be done by adding $p$ to $y$ -coordinate $k$. That is,
$\left( {h,k + p} \right)$. Substituting the values of $h,k$ and $p$ in the formula and we get,
$\left( {0, - 4 + \dfrac{1}{4}} \right) = \left( {0, - \dfrac{{15}}{4}} \right)$
So, focus of parabola is $\left( {0, - \dfrac{{15}}{4}} \right)$-----(3)
We now find the axis of symmetry by finding the line that passes through the vertex and the focus.
$x = 0$-----(4)
The directrix of a parabola is the horizontal line which can be found by subtracting $p$ from $y$- coordinate $k$ of the vertex if parabola opens up or down i.e., $y = k - p$. By substituting the values
of $p$ and $k$ we get,
$y = - 4 - \dfrac{1}{4}$
$y = - \dfrac{{17}}{4}$-----(5)
From equation (1), (2), (3), (4) and (5) we can say,
Direction: Opens up
Vertex: $\left( {0, - 4} \right)$
Distance: $\dfrac{1}{4}$
Focus: $\left( {0, - \dfrac{{15}}{4}} \right)$
Axis of symmetry: $x = 0$
Directrix: $y = - \dfrac{{17}}{4}$
Let us find out some points by putting different values of $x$.

$x$	$- 2$	$- 1$	$0$	$1$	$2$
$y$	$0$	$- 3$	-4	$- 3$	$0$

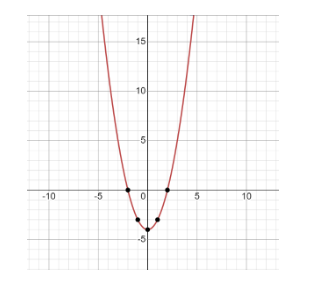
Thus, this is our required graph.

Note: Since the given equation of parabola includes linear $x$ and $y$ terms, then the vertex of the parabola can never be the origin. In such a case, the vertex has to be found by simplifying the equation into its standard form. If the parabola is ${x^2} = 4ay$, then the vertex of the parabola will be the origin.