Question

How do you graph the number $7 - 5i$ in the complex plane and find its absolute value?

Answer 1

Hint : We have been given a complex number. We have to plot this number as a point in the complex plane. A complex plane is a coordinate system where one axis represents the real part and the other axis represents the imaginary part. The absolute value of a complex number $\left( {a + bi} \right)$ can be found using the formula $\sqrt {{a^2} + {b^2}}$ .

Complete step by step solution:
We have to plot the complex number $7 - 5i$ in the complex plane.
A complex plane is a coordinate system with x-axis representing the real part and the y-axis representing the imaginary part.
To find the real and the imaginary part, we compare the given complex number with $a + bi$ .
In a complex number, the terms associated with $i$ is the imaginary part, and the other term is the real part, i.e. $a$ is the real part and $b$ is the imaginary part. Thus, the coordinates of the complex number $\left( {a + bi} \right)$ is $\left( {\operatorname{Re} (z),\;\operatorname{Im} (z)} \right)$ or $\left( {a,\;b} \right)$ .
Let us represent the given complex number as $z = 7 - 5i$ .
Here the real part of $z$ , denoted as $\operatorname{Re} (z)$ , is $7$ . And the imaginary part of $z$ , denoted as $\operatorname{Im} (z)$ , is $- 5$ .
Now we plot the number. For this we have to plot the coordinate $\left( {7,\; - 5} \right)$ on the complex plane.
This is as shown below by point A,

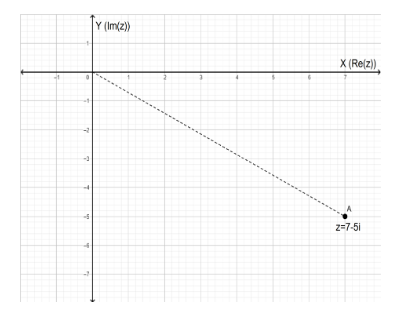
Now we have to find the absolute value of the given complex number.
For a complex number $z = \left( {a + bi} \right)$ , the absolute value is given as $\left| z \right| = \sqrt {{a^2} + {b^2}}$ .
Thus the absolute value of the given complex number $7 - 5i$ is $\sqrt {{a^2} + {b^2}} = \sqrt {{7^2} + {{\left( { - 5} \right)}^2}} = \sqrt {49 + 25} = \sqrt {74} \approx 8.602$

Note : We plotted the given complex number simply as a coordinate point on the complex plane where the coordinates are taken as $\left( {\operatorname{Re} (z),\;\operatorname{Im} (z)} \right)$ . Notice that the formula for absolute value is similar to that of the distance formula. In a way, the absolute value represents the distance between the origin and the point representing the complex number on the graph.