Question

How do you graph the line $y=\dfrac{1}{3}x-2$?

Answer 1

The given equation of the line is in the form of $y=x$. Therefore, by transforming the graph of the line $y=x$ we can graph the given equation $y=\dfrac{1}{3}x-2$. For this, we have to first shift the graph of $y=x$ two units to the right in the horizontal direction to obtain the graph of $y=x-2$. Then we need to expand the graph of $y=x-2$ three units in the horizontal direction to finally obtain the required graph of $y=\dfrac{1}{3}x-2$.

Complete step by step solution:
The equation of the line given in the above question is
$\Rightarrow y=\dfrac{1}{3}x-2$
We can observe that the above equation is similar to the equation $y=x$. Therefore we use the graph of the line $y=x$ as a basic graph, which is drawn as shown below.

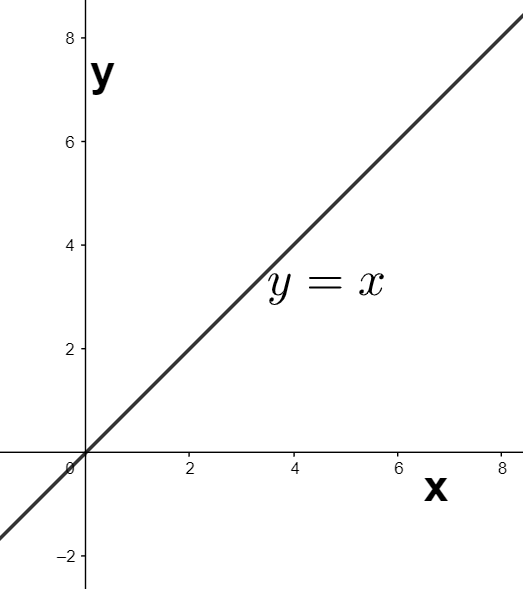
Now, we consider the graph of the equation $y=x-2$. We can see that on changing the independent variable form $x$ to $x-2$, we will obtain the equation from $y=x$ to $y=x-2$. Therefore, the graph of the equation $y=x-2$ can be obtained by shifting the above graph of the equation $y=x$ two units to the right as shown below.

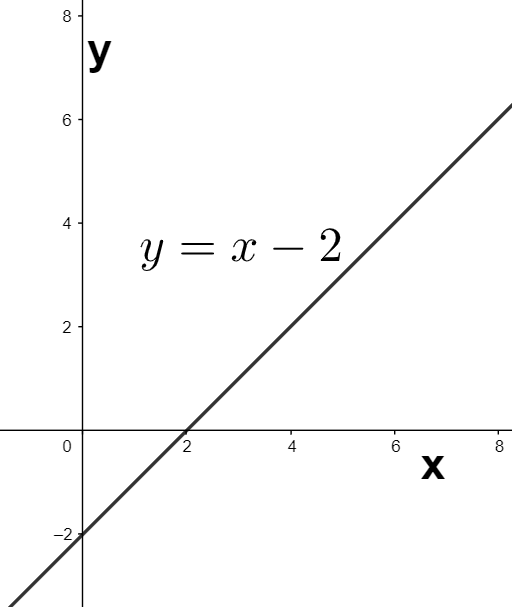
Finally, we change the independent variable from $x$ to $\dfrac{1}{3}x$ so as to obtain the equation of the line as $y=\dfrac{1}{3}x-2$ from the equation $y=x-2$. Since the independent variable is changed from $x$ to $\dfrac{1}{3}x$, the graph of $y=x-2$ can be expanded three units in the horizontal direction to obtain the required graph of $y=\dfrac{1}{3}x-2$ as shown below.

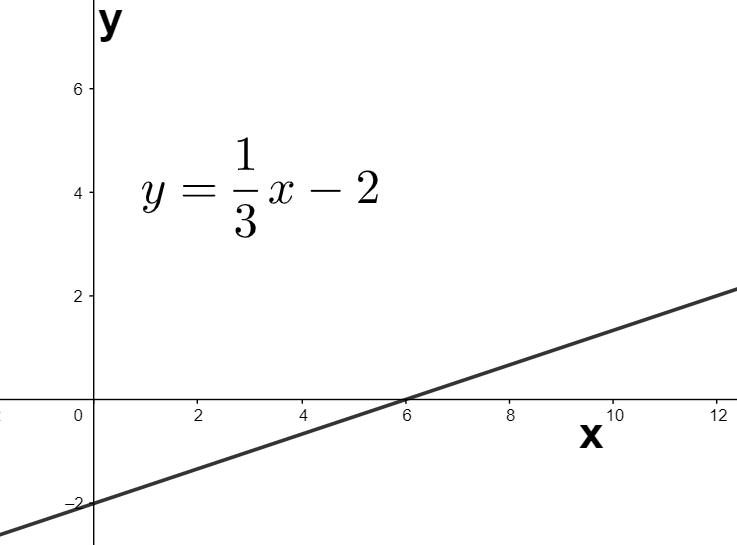
Hence, we have graphed the given equation $y=\dfrac{1}{3}x-2$.

Note: We can also shift the graph of the equation $y=x$ two units downwards to obtain the graph of $y=x-2$. Also, we must remember that we have to perform the shifting first and then the scaling for solving these types of questions.