Question

How do you graph the line$y = - 3$?

Answer 1

This question is from the topic of graphs. In this question we have to plot the line $y = - 3$. Given the equation of line $y = - 3$ did not have $x$ component. As we know that any equation of line is of the form $ax + by = c$. To solve this question we will first write this equation in the slope-intercept form of line to find some points which lie on the line $y = - 3$.

Complete step by step answer:
Let us try to solve this question in which we are asked to plot the graph of line $y = - 3$. To plot this graph we will first write the equation of the given line $y = - 3$ in slope-intercept form of line which is $y = mx + c$. After doing this we will find some points which lie on the line $y = - 3$ with the help of these points we draw the graph. Now, given the equation of the line $y = - 3$ will be written in slope-intercept form as $y = 0x + ( - 3)$.

Given equation slope and intercept are given by $m = 0$ and $c = - 3$.Now, we will find some point which lies on the given equation by putting values of $x$and $y$respectively.
$y = 0x + ( - 3)$ $(1)$
Let us take $x = 0$ then the value of $x$ in equation$(1)$, we get $y = - 3$.
Similarly, Let us take $x = 1$ then the value of $x$ in equation$(1)$, we get $y = - 3$.
Similarly, Let us take $x = 2$ then the value of $x$ in equation$(1)$, we get $y = - 3$.
Similarly, Let us take $x = - 1$ then value of $x$ in equation$(1)$, we get $y = - 3$.
Similarly, Let us take $x = - 2$ then value of $x$ in equation$(1)$, we get $y = - 3$.Now we have some points which lies on $y = - 3$, here is the graph

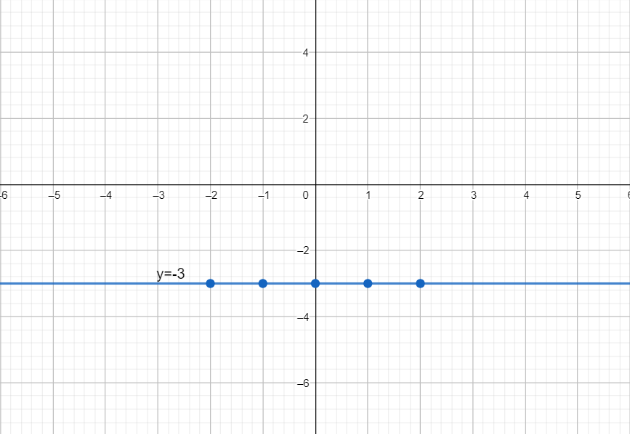
These blue dots on the line are above points which we have used to draw the line.

Note: From the graph of line $y = - 3$ is parallel to $x - axis$.Questions in which we are asked to plot the graph of a line. First write the given equation of line in slope intercept form. Then find some points which lie on the line.