Question

How do you graph the line $x-4y=18$ ?

Answer 1

Problems on graphing linear equations can be easily done by comparing the given equation of straight line with the general equation of a straight line, which is $y=mx+c$ . After comparing the given equation with the general equation of the straight line, we get the slope and the $y$ -intercept, of the straight line. Knowing these two parameters, the given straight line can be easily drawn.

Complete step-by-step solution:
The given equation is
$x-4y=18$
First of all, we recognize that this is a linear equation, so it is an equation of a straight line.
Now, we must convert this equation into the slope and intercept form of a straight line. To do so we keep the term associated with y to the left-hand side and the rest to the other side as shown below
$\Rightarrow 4y=x-18$
Dividing both sides of the equation by $4$ we get
$\Rightarrow y=\dfrac{1}{4}x-\dfrac{18}{4}$
$\Rightarrow y=\dfrac{1}{4}x-\dfrac{9}{2}....\left( 1 \right)$
The general slope-intercept form of a straight line is
$y=mx+c$
Where, $m$ is the slope of the line and $c$ is its $y$ -intercept.
Comparing the equation $\left( 1 \right)$ with that of the general slope-intercept form, we get
$m=\dfrac{1}{4}$ and $c=-\dfrac{9}{2}$
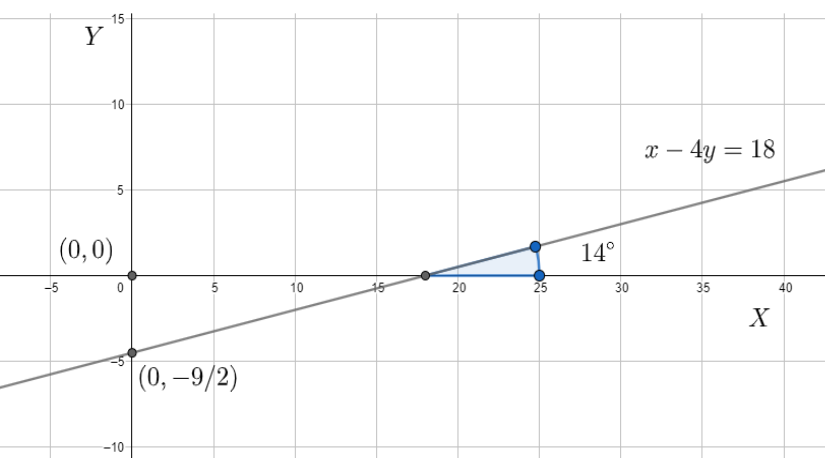
$y$ -intercept $-\dfrac{9}{2}$ means that the point where the line intersects the $y$ -axis, is $\left( 0,-\dfrac{9}{2} \right)$ .
Slope of a line means the tangent of the angle that the line makes with the positive $x$ -axis in an anticlockwise direction. If we have the value of the slope, we can find the angle which the line makes by the equation,
$\theta ={{\tan }^{-1}}m$
The angle made by this line with the $x$ -axis then, will be
$\Rightarrow \theta ={{\tan }^{-1}}\dfrac{1}{4}$
$\Rightarrow \theta ={{14}^{\circ }}$
Then, we draw a line at origin which makes this $\theta$ angle with the positive $x-axis$ in the anticlockwise direction.
Therefore, we can conclude that the last line that we have drawn is nothing but our required line.

Note: To graph the given line we require geometrical apparatus like a protector and scale, so while using these tools we must keep the values as accurate as possible to avoid inaccuracy. Also, this problem can also be solved without comparing the equation to its general form. We find and plot any two pints that lie on the given line and connect the points using a scale to get the straight line.