Question

How do you graph the line $x + 3y = 3$ ?

Answer 1

Hint : We will use intercept form to determine the points of the given equation. And, we will also solve this question by assuming the value of $x = 0$ , by applying the value of $x$ , we will get the coordinate of $y$ . Then, we will assume the value of $y = 0$ , by which we will get the $x$ coordinate. Finally, we will plot the points in the graph.

Complete step-by-step answer :
Here, we will graph $x + 3y = 3$ .
Now, we will write the equation in the slope- intercept form i.e., $y = mx + b$ $\to \left( 1 \right)$
Where the $m$ is the slope
$b$ is the $y$ - intercept
Then, we have $3y = 3 - x$
$y = \dfrac{{3 - x}}{3}$
$y = \dfrac{3}{3} - \dfrac{x}{3}$
$y = - \dfrac{1}{3}x + 1$ $\to \left( 2 \right)$
By comparing equation $\left( 1 \right)$ and $\left( 2 \right)$ , we have
$m = - \dfrac{1}{3}$ i.e., the slope of the equation
$b = 1$ i.e., the $y$ - intercept
The $y$ - intercept is the point where the line intersects the $y$ -axis.
Therefore, the point is $\left( {0,1} \right)$ .
Slope is the ‘steepness’ of the line, also commonly known as rise over run i.e., $\dfrac{{rise}}{{run}}$ . Here, $m = - \dfrac{1}{3}$ therefore, we can say that the graph “rise” $- 1$ point upwards and “run” $3$ points to the right from the $y$ - intercept.
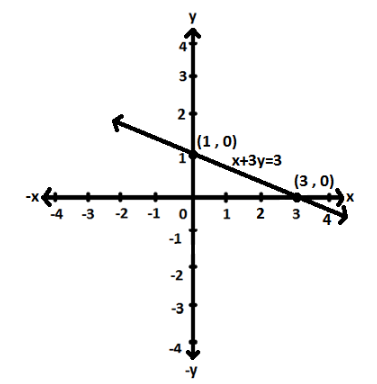
Now, we know the slope and the $y$ - intercept, thus we also know that $\left( {0 + 3,1 + \left( { - 1} \right)} \right) = \left( {3,0} \right)$ which will also be on the line.
Now, we know two points of the equation i.e., $\left( {0,1} \right)$ and $\left( {3,0} \right)$ .
Let us plot these points graphically,

Alternate method:
Now, the given equation is $x + 3y = 3$ .
Let us consider $x = 0$ , by substituting we have,
$0 + 3y = 3$
$3y = 3$
$y = \dfrac{3}{3}$
$y = 1$
Therefore, the point is $\left( {0,1} \right)$ .
Now, let us consider $y = 0$ , by substituting we have,
$x + 3\left( 0 \right) = 3$
$x + 0 = 3$
$x = 3$
Therefore, the point is $\left( {3,0} \right)$
Hence, the points are $\left( {0,1} \right)$ and $\left( {3,0} \right)$ .
Now, let us plot the points graphically,

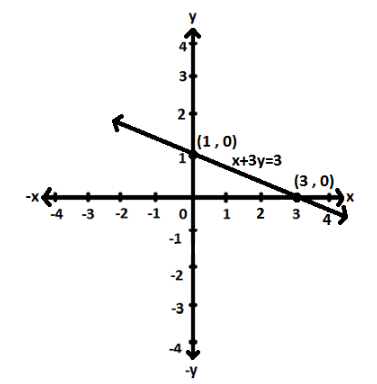
Note : Equation of straight line is usually written in the slope-intercept form. When we are given an equation in slope- intercept form, we can use the $y$ - intercept as the point, then out the slope from there. When an equation of a line is not given in slope-intercept form, our first step will be to solve the equation for $y$ . Sometimes the slope intercept form will be called as $y$ -form.