Question

How do you graph the line $-x-3y=2$ ?

Answer 1

We know that the equation of a straight line is y = mx + c and we can represent the equation of straight line in another form $ax+by=c$ , we can convert this into y = mx + c where m is the slope of line and c is the y intercept of the straight line.

Complete step by step answer:
The given equation of the line is $-x-3y=2$
We can draw the graph of the straight line by joining any 2 points which are on the line or satisfy the equation of line
So let’s choose any 2 points which are on the straight line $-x-3y=2$
Let’s take x equal to 0 so the value of y will be $-\dfrac{2}{3}$
So one point is $\left( 0,-\dfrac{2}{3} \right)$
For another point let’s take y equal to 0, so the value of x equal to – 2
So another point is $\left( -2,0 \right)$
So the graph of $-x-3y=2$ will joining the points $\left( 0,-\dfrac{2}{3} \right)$ and $\left( -2,0 \right)$ and extend the line infinitely

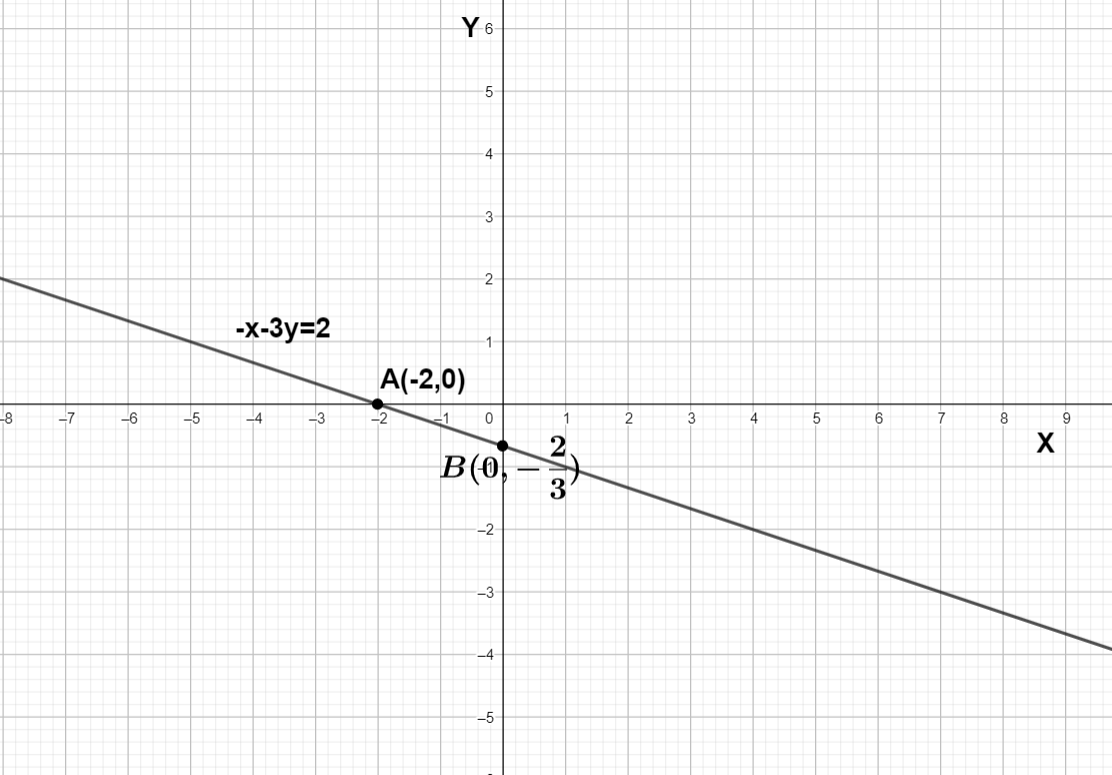
We can see the graph of $-x-3y=2$ is the straight line joining 2 points A $\left( -2,0 \right)$ and B $\left( 0,-\dfrac{2}{3} \right)$

Note:
We can write all the lines in the form y = mx+ c except all the lines which are parallel to the Y axis. The reason behind it is the slope of all the lines which are parallel to the Y axis tends to infinity. The equation of all such lines is x=k where k is a constant.